疫情下的大数据力量!

大数据产业创新服务媒体
——聚焦数据 · 改变商业

新型冠状肺炎病毒(2019-nCoV)从2019年12月26日被发现,到当月31日官方公告新型肺炎,再到2020年2月4日16时21分,全国已有20503人确诊,426人死亡。这次病毒疫情正在以2003年非典型肺炎(SARS)五倍的速度在扩散,有人甚至将这个病毒的危害程度与1918年西班牙流感进行百年大病毒对比。
目前新的确诊患者人数还在逐日增加,但全国已经众志成城,从扩散速度的顶峰到下降应该为期不远了,发病率预计在正月十五(2月8号)前后可能出现回落。知名传染病专家桂希恩预测,正月十五前武汉肺炎疫情可能出现拐点。上海市医疗救治专家组组长张文宏教授断言,控制新冠病毒感染的主体战役应该在1个月内结束,2个月内进入尾声。
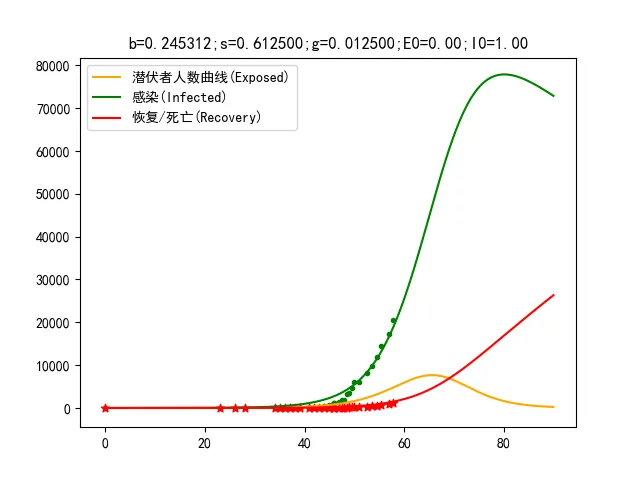
本文以2020年1月以来国家疾控中心公布的感染统计数字为基础,对国际上流行的传染疾病传播模型SEIR(Susceptible, Exposed, Infected, Recovered)进行拟合,通过病毒潜伏者(Exposed)数量随时间变化的曲线预测2月11日扩散速度可能出现顶峰然后开始下降。


1)基本再生数(R0)指一个病毒携带者,进入易感人群中后可感染的二代病例个数。
2)根据Kermack与McKendric【1】的推算,当基本再生数R0 持续小于 1时,新增感染数会随时间最终收敛到0。也就是说此时病毒会自行消亡,不再构成传染病威胁。
3)基本再生数的基本式【2】:R0 = r* c * d 。其中 r 是指病毒传播性(病毒携带者将病毒传染给被接触者的可能性),c 指的是易感人群和病毒携带者之间的平均接触率,d指的是预期感染持续时间。本模型使用该基本式对病毒扩散随时间的变化的趋势(扩散趋势)进行推导。
4)我们有理由认为所有发病的病毒携带者和已被发现的病毒携带者都已被隔离,且被隔离的病毒携带者不在可能的接触范围内,因此我们需要关注的是未被发现的病毒携带者(UnquarantinedExposed)的扩散趋势。假设病毒潜伏者(Exposed)被发现的第一时间就受到隔离,我们可以用模型仿真估算所得的病毒潜伏者(Exposed)数量随时间变化的曲线(潜伏者曲线)来代表未被发现的病毒潜伏者占总接触人数的比例(UnquarantinedExposed Rate)随时间变化的趋势。
5)如果不考虑在仿真时间段(2月4日至2月12日)接触环境、保护措施的改变,我们可以假设:病毒的传播性(r)不随时间变化,并且预期感染持续时间(d)为固定值。从而,未被发现的病毒携带者扩散趋势与易感人群和病毒携带者之间的平均接触率(c)一致。


针对确诊病例、疑似病例、当日增长确诊病例、当日增长疑似病例进行多项式回归。 对武汉肺炎病毒建立SIR模型,对1月1日至1月31日期间病例数进行仿真,与多项式回归结果和真实值比较,建立对感染率、康复率和易感人数等参数的直觉模型。 对武汉肺炎病毒建立SEIR模型,搜索拟合1月1日至2月3日感染、治愈/死亡患者数的最优模型参数,对2月4日以后进行模拟仿真,估算病毒潜伏者曲线的趋势。
2019数据猿年度榜单: