架构设计分析报告:稀疏组合性——深度神经网络泛化能力的底层基石

1. 理论引言：从工程应用到理论“麦克斯韦方程组”

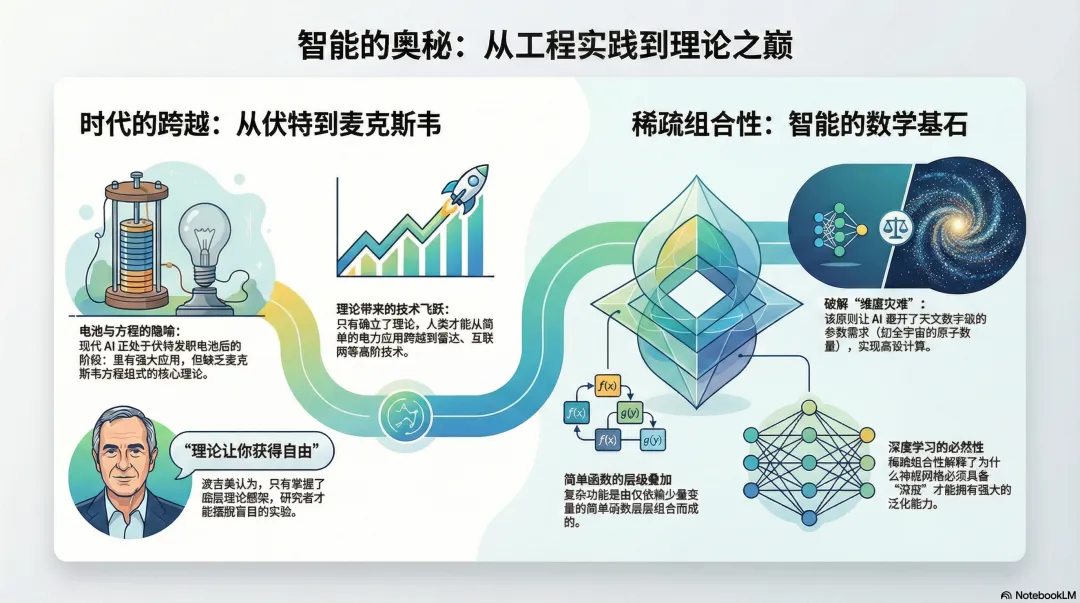
在当前的深度学习范式中，我们正处于一个典型的“伏打（Volta）时代”：工程实践凭借直觉与算力堆砌，在缺乏严密理论指导的情况下制造出了极其高效的“智能电池”。正如 1800 年伏打发明电池后，人类在尚未理解电磁本质前便已开发出电机与照明系统，目前的深度神经网络架构依然依赖于经验主义的摸索。

然而，从工程优势向理论领航转化的临界点已经到来。首席算法架构师必须意识到，我们迫切需要一套属于深度学习的“麦克斯韦方程组”，以解释模型为何能在极高维空间中实现超凡的泛化。计算神经科学家 Tomaso Poggio 的研究指明，深度学习的成功并非偶然，而是通过其层级化结构在数学上成功捕捉了“稀疏组合性（Sparse Compositionality）”这一物理世界的底层归纳偏置（Inductive Bias）。本报告旨在剖析这一核心原理，将其转化为可量化的架构设计逻辑。

--------------------------------------------------------------------------------

2. 维度诅咒：神经网络面临的计算极限

在设计处理高维输入（如图像或自然语言）的系统时，架构师首先要面对的是物理意义上的不可计算性。

2.1 规模化的指数爆炸

以处理一张32×32像素的极小图像为例，其输入变量数d=1000。

•参数需求：传统的函数近似（Function Approximation）理论指出，若要以 10% 的精度近似一个平滑的千维函数，所需的参数量（即存储或计算单元）可能高达101000。

•物理极限对比：已知宇宙中的质子总数约为1080。这意味着，若不改变计算结构，即便是动用全宇宙的原子，也无法构建出一个能有效处理千维输入的通用近似器。

2.2 传统假设的软弱性

依赖于“平滑性（Smoothness）”的传统数学假设无法解决上述指数爆炸问题。在物理极限面前，单纯的连续性无法提供足够的约束。因此，架构师的任务必须从“暴力拟合”转向“结构性分解”，寻找能够规避维度诅咒的必然路径。

--------------------------------------------------------------------------------

3. 稀疏组合性：复杂函数的分解逻辑与图灵可计算性

稀疏组合性不仅是一种设计偏好，更是“高效可计算性”的数学先决条件。

3.1 “函数之函数”与图灵可计算性

Poggio 提出了一个深刻的洞见：如果一个任务能在非指数级时间内被图灵机（或计算机）处理，那么该函数在数学上必然是可分解的，即表现为“函数之函数（Functions of Functions）”的递归结构。

从计算底层的角度看，真实世界中并不存在所谓的“实数（Real Numbers）”，一切计算最终都回归到布尔原语（AND, OR, NOT）的组合。因此，任何复杂的全局函数本质上都是由一系列子函数嵌套而成的稀疏结构。

3.2 严苛的“稀疏预算”

架构师在设计子模块（如卷积核或注意力头）时，必须遵循明确的变量约束，以确保计算的高效性：

•布尔变量约束：每个子函数依赖的变量应少于 40 个。

•非布尔变量约束：每个子函数依赖的变量应少于 14 个。当每个计算单元仅处理这种规模的局部变量时，整体计算规模将从“指数级”塌缩至“多项式级”。

3.3 二叉树结构与局部感受野

这种分解逻辑在架构上最直观的体现是层级化的二叉树模型。通过将输入划分为局部 Patch，并在层级间逐步合成全局表征，深度网络在数学上完美映射了复杂系统的“分而治之”逻辑。

--------------------------------------------------------------------------------

4. 架构优势对比：深度网络 vs. 浅层网络

从架构演进的角度看，深度架构的出现是数学约束下的必然选择，而非单纯的参数堆叠。

架构决策的必然性：如果一个目标函数具有稀疏组合结构，深度网络在数学上是唯一能够实现“多项式级参数近似”的方案。卷积神经网络（CNN）通过参数共享和局部连接，本质上是在物理层面上强制执行了稀疏组合性的约束。

--------------------------------------------------------------------------------

5. “调节旋钮”的逻辑：参数规模与泛化能力

泛化能力的本质在于如何通过减少“有效自由度”来防止模型死记硬背训练数据。

5.1 旋钮理论与过拟合规避

Poggio 将模型参数比作“旋钮（Knobs）”。稀疏组合性通过减少必须调整的旋钮数量，确保了模型是在学习底层的组合逻辑而非随机噪声。这种结构化的约束使得模型在面对从未见过的输入组合时，依然能通过其内部的子函数逻辑进行正确推理。

5.2 Transformer 与自回归框架的特例分析

Transformer 架构的成功揭示了学习“构成函数（Constituent Functions）”的新路径。

•中间数据供给：在标准深度网络中，我们只有全局的输入与输出。但在 Transformer 的自回归（Auto-regressive）训练中，“预测下一个词（Next-token Prediction）”实际上为每一个层级、每一个构成函数提供了监督信号。

•逻辑链路：这种训练模式为函数的级联分解提供了中间数据流，使得复杂的语言层次结构能够通过组合逻辑被逐层学习，从而在海量数据中实现了前所未有的泛化效果。

5.3 生物学印证

视觉皮层从 V1（提取简单特征）到 IT 区（识别复杂物体）的层级结构，正是生物进化对现实世界稀疏组合结构的适应。大脑通过层级化的稀疏连接，以极低能耗解决了原本不可计算的高维视觉识别问题。

--------------------------------------------------------------------------------

6. 结论：架构师的理论武装

理解稀疏组合性不仅是学术探讨，更是决定算法上限的战略资产。

6.1 战略行动建议

1.识别任务的组合先验：在启动架构设计前，应分析目标任务是否具有天然的局部相关性或层级化特征。

2.结构化深度优先：面对复杂任务，应优先增加网络深度（增加函数嵌套层次）而非单层宽度，以匹配任务的组合复杂度。

3.强化稀疏约束：优化模型时，应优先采用具有局部感受野或稀疏注意力机制的连接方式，严控单个神经元的变量摄入量（遵循 <40/14 原则）。

6.2 未来展望与 Pascal 赌注

面对 AGI 的热潮，架构师应保持理性。借鉴**“帕斯卡赌注（Pascal's Wager）”**：由于我们无法证明超级智能是否会短期内全面接管，最理性的方案是赌“人机协作将持续很长时间”，并据此深耕底层理论。

正如 Garcia Marquez 所言，飞机的飞行速度让人的灵魂跟不上脚步，产生了一种“教育上的时差（Jet lag for education）”。AI 的演进速度已远超当前的教育与社会适应速度。在这种大环境下，坚守稀疏组合性这一连接生物大脑与人工网络的桥梁，将是我们构建可解释、可泛化且安全的智能系统的基石。

总结：智能之所以可计算，是因为世界本身是可分解的。稀疏组合性是算法架构师在对抗维度诅咒时，手中掌握的最强有力、也是唯一的数学武器。