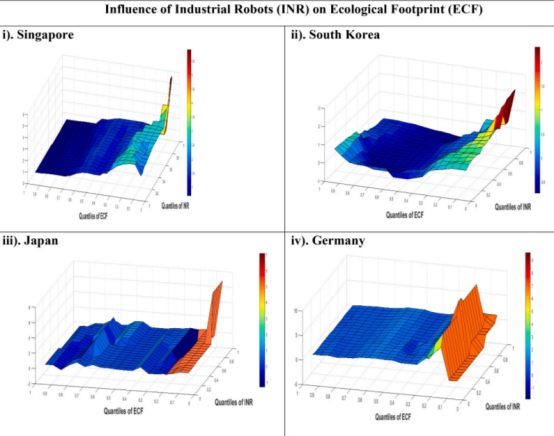
注:y轴表示生态足迹分位数,x轴表示工业机器人分位数,z轴表示实测斜率系数α1(θ,τ)。图表右侧的颜色表示斜率系数,从蓝色(表示低值)到红色(表示最高值)。深红色表示INR和ECF之间存在强烈的正相关关系,而深蓝色则表示存在显著的负相关关系。
文献来源
原文题目:Robots for sustainability: Evaluating ecological footprints in leading AI-driven industrial nations
原文作者:Lei Liu, Zeeshan Rasool, Sajid Ali, Canghong Wang*, Raima Nazar
第一作者单位:Teaching and Research Department of the Party’s Youth Movement History, China Youth University of Political Studies
通讯作者单位:School of Accounting and Finance, Xi’an Peihua University
原载单位:Technology in Society
发表时间:2024年3月
观点摘要
近几十年来,将工业机器人(Industrial Robot, INR)集成到制造流程中已经彻底改变了生产流程。这些机器可以显著影响全球经济社会的众多特征,甚至超出单纯的经济影响,涉及了例如生态足迹(Ecological Footprint, ECF)等环境议题。通过精确和高效地自动化任务,工业机器人有助于最大限度地减少资源利用和排放以及生态足迹。但同样的,工业机器人的制造和部署可能会对环境产生不利影响,如生产机器人的部件可能涉及稀有金属和矿物的开采和冶炼,处置废弃、故障的机器人可能会导致电子垃圾,也对回收和处置提出了挑战。所以,在走向可持续发展的未来的道路上,寻求技术扩张和环境问题之间的平衡显得至关重要。本文以2007年至2020年10个主要工业人工智能国家为样本,来评估特定国家的工业机器人使用对生态足迹的影响。这种方法提供了全面的全球视角,同时提供了与每个国家相关的量身定制的见解。
研究发现:使用工业机器人能通过降低不同数据分位数的生态足迹来提高环境质量。例如在在日本和德国,研究发现INR与ECF呈现显著的负相关,表明工业机器人通过降低日本和德国中低至最高等级的生态足迹来提高环境质量。但除此之外,在工业机器人总分位数与日本和德国最低的生态足迹分位数相结合的地区,工业机器人和生态足迹之间存在着正相关,表明工业机器人会通过增加较低污染水平下的生态足迹来降低环境质量。在法国,INR和ECF之间存在混合关系,INR与ECF的显著负相关只在ECF分位数较高的地区显现,而在ECF水平居中的地区,INR反而与ECF展现出显著的正相关关系;同法国一样,意大利也存在这种混合关系。只有意大利INR分位数水平较高的地区,才展现出INR与ECF的显著负相关,从而改善地区环境,相比之下,在INR分位数水平处于低位的地区,发现了INR与ECF之间的显著正相关。在工业化的高级阶段,INR通过降低ECF大大改善了环境质量。然而,在中低工业化水平下,这些机器人往往会增加ECF,对环境质量产生不利影响。
基于以上研究,提出以下建议:在INR高分位数的经济体,政策制定者应鼓励在生态影响较大的行业投资更复杂、更高效的机器人技术,并将其与绿色实践和可再生能源相结合,用以扩大其环境效益。制定教育和培训计划,使劳动力为更加自动化的工业环境做好准备。此外,政策制定应具有适应性,允许根据不同地区对INR的生态影响和经济表现的持续监测进行调整,确保这些举措在支持经济增长的同时有效地减少ECF在工业化水平较高的国家,如日本、韩国和德国等应强制要求考虑采用INR的企业进行环境影响评估,特别是在与较高ECF水平相关的行业,有助于确定潜在的环境风险并制定相关战略。
研究展望
本研究存在以下局限性,可以为该领域的未来研究提供有价值的指导。第一,本文只关注了ECF,而不包括CO2、SO2、N2O和CH4等温室气体排放。在未来的研究中,在考虑环境代理变量的时候,纳入这些指标可能有利于发现不同的研究结果。未来的研究可以探索数据来源和指标,例如来自政府间气候变化专门委员会(IPCC)或国家环境机构等知名机构的排放数据。第二,探索几个经济集团(如G20、中东和北非地区、欧盟和G7)之间INR和ECF之间的联系,可能会显著提高公众对这种联系的认识。通过在这些不同的背景下进行深入调查,我们可以获得关于不同地区INR和ECF之间联系的潜在变化的有价值的观点。第三,分位数回归法在强制添加部分控制变量时面临问题。为了解决这一限制,未来的工作将探讨多变量技术的集成,如分位数ARDL建模,这可能会提供对关系的全面认识。
整理发布
章志诚 浙江工业大学2022级应用经济学硕士研究生




