铝合金薄板含胶滚压成形工艺建模及实验

机器人滚边是车身门盖件制造的重要工艺.利用机器人驱动滚轮，使外板翻边部分逐段发生塑性变形从而将内板压合包住，实现内外板连接[1].铝合金材料大量应用于车身和门盖件中以实现轻量化，但其在滚压发生大变形时易产生裂纹，因此需要采用多道次滚压.一方面，滚压工艺中引入的非金属折边胶，其理化性质与金属材料有较大不同，滚压过程中易流动，且会与金属板材产生异质耦合作用.另一方面，相对于传统模具压合，机器人滚压时板材逐段发生塑性变形，每个轨迹点的滚边压力和角度均发生变化，导致板材表面易产生波浪起皱、翘曲和缩进涨出等缺陷，极大影响表面成形质量.以上问题增加了含胶铝合金滚压成形机理及其成形质量的研究难度.因此，面向门盖件制造质量持续提高，进行铝合金薄板含胶滚压成形工艺建模及成形质量控制研究具有良好的理论研究意义和工程应用背景.

薄板含胶滚压属于多工步成形工艺范畴，韩飞等[2]研究超强钢多道次辊弯成形，设计3组道次数不同的辊弯成形试验，从成形角度和道次数等方面阐明回弹角度的变化规律.李雪龙等[3]以铝合金半球形构件普旋的首道次预成形阶段为例，基于能量法建立法兰起皱预测模型.针对多道次滚压成形质量，国内外学者做了大量研究，Le Mao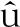

然而，在材料和物理化学属性方面，滚压胶黏剂与薄板金属相差巨大；在滚压过程中，胶层流动行为及其与金属板材的异质耦合作用，显著增加了含胶滚压成形数值模拟的研究难度.相对于滚压道次研究，目前针对含胶薄板的滚压工艺研究较少.李建军等[17]引入光滑粒子法模拟胶黏剂，建立含胶铝合金薄板滚压模型，研究了胶层黏度、挤压速度和胶层厚度参数对成形质量的影响.徐文欢[18]研究了折边胶在滚边生产加工过程中的涂覆质量和控制措施.综上所述，目前滚压工艺研究主要集中在异质无胶薄板滚压方面，而对于胶层引入后，如何模拟胶层流动以及如何定量研究胶层与金属薄板交互作用等机理的研究较少.因此，亟需建立轻合金含胶滚压成形数值模拟的有效模型.

为此，基于有限元-光滑粒子流体动力学法(FEM-SPH)建立铝合金薄板含胶滚压成形分析模型，进行含胶铝板两道次滚压数值模拟，并搭建双滚轮机器人滚压实验系统进行对比实验，验证所建模型的有效性.设计正交试验研究TCP-RTP值、滚轮直径、翻边高度和圆角半径4个关键工艺参数对滚压成形质量的影响及首末道次之间的质量指标变化.最后进行工艺参数与质量指标之间的数据拟合，为含胶薄板滚压成形机理及其质量预测提供依据.

为了研究引入胶层后的铝合金薄板滚压成形机理，提出基于FEM-SPH的含胶薄板滚压成形分析模型，如图1所示.其中，粒子近似式[19]和罚函数接触算法分别为

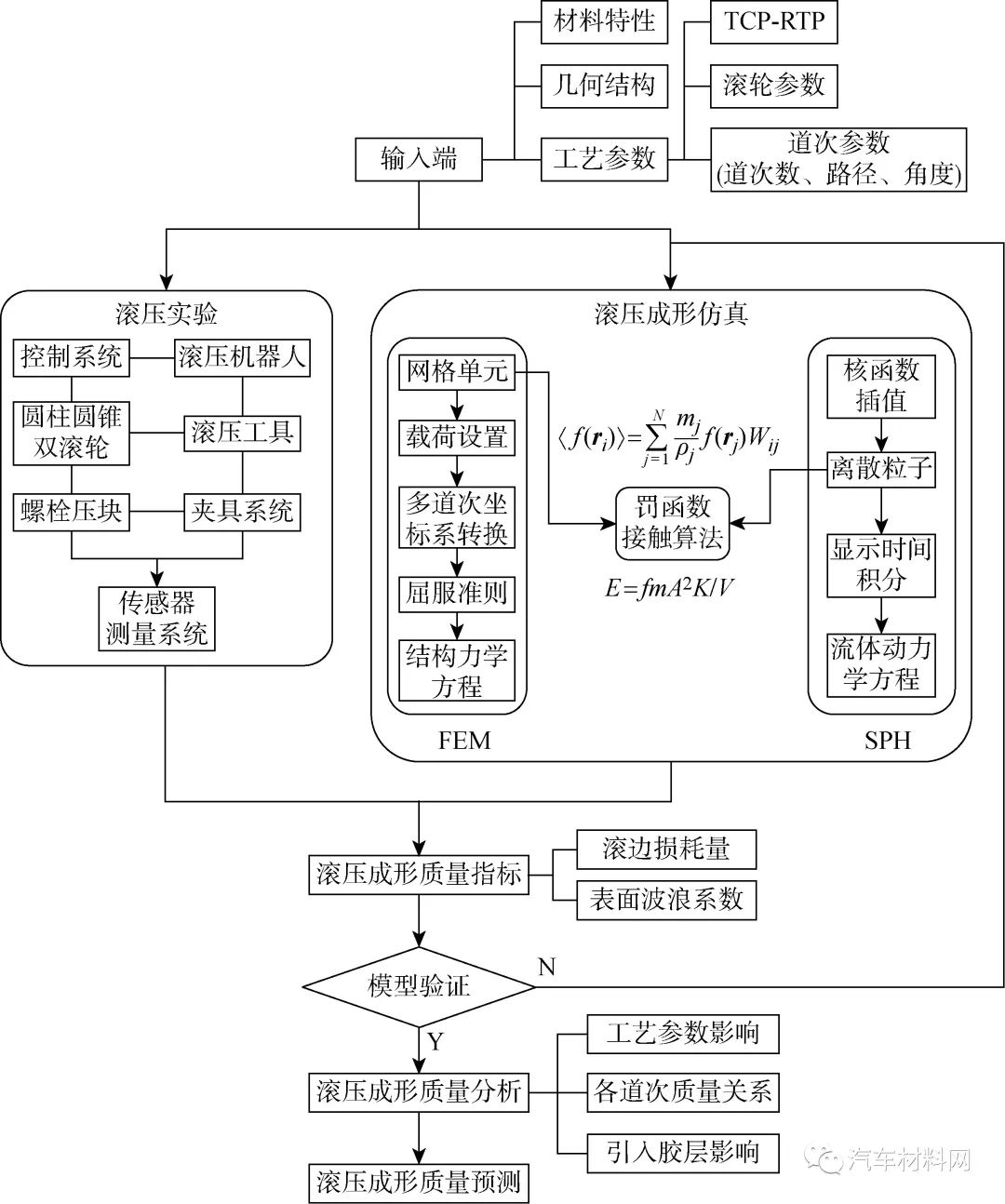
图1 铝合金薄板含胶滚压成形分析模型

Fig.1 Analysis model of roll-forming of aluminum alloy sheet with adhesive

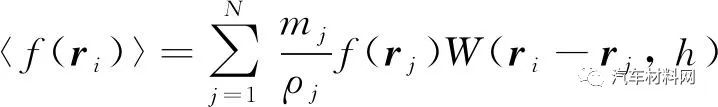
(1)E=fmA2K/V

(2)式中：〈f(ri)〉为任意函数f(r)在粒子i处的粒子近似式；mj、ρj和N分别为支持域内粒子的质量、密度和数量；Wij=W(ri-rj, h)为核函数，具有多种形式，本文选用Abaqus中默认的Cubic核函数；ri和rj为支持域内的任意两个位置向量点；h为粒子支持域的光滑长度；E为接触刚度；f为惩罚比例因子；m为默认主比例因子；A为接触面积；K为接触单元体积模量；V为接触体积.

以实验与仿真相结合的方式，利用Abaqus 2019建立有限元仿真模型，进行含胶薄板两道次滚压数值模拟.利用铝合金薄板含胶双滚轮滚压对比实验，验证分析模型的有效性.研究滚压工艺质量，包括关键工艺参数对滚压质量的影响以及首末滚压道次之间的质量变化.最后进行滚压质量预测，为实际生产中的滚压成形工艺质量控制优化提供参考.

1.1 薄板滚压变形分析

在薄板件翻边滚压过程中，随着弯曲程度的增大，板件会从弹性变形逐渐转变为塑性弯曲变形，如图2所示.在板件弯曲初始阶段，外板件受拉，内板件受压，受力较小，板件发生弹性变形，满足胡克定律；塑性变形发生在板件大变形处，满足Tresca屈服准则；在滚压阶段即将完成时，板料内层、外层和中心的切应力均大于屈服强度，板件进入纯塑性弯曲阶段.

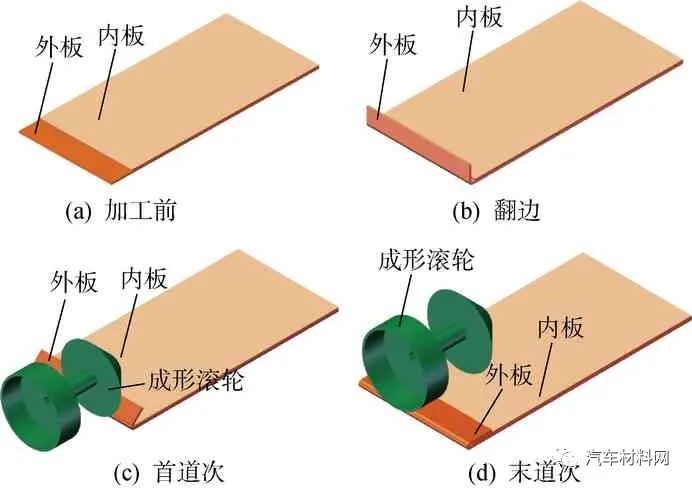
图2 板件变形过程示意

Fig.2 Schematic diagram of sheet deformation process

1.2 FEM-SPH法

板材属于连续体，利用传统FEM可以较好分析其在受外载荷条件下的成形过程；而胶层属于流体，其在滚压时发生大变形，处于流动状态，利用SPH法的模拟精度较高.SPH法是一种基于粒子的无网格拉格朗日法，利用FEM-SPH耦合法进行含胶薄板结构的滚压仿真，将胶层离散为有限个带有物质属性的粒子，通过支持域内粒子核函数近似的形式求得粒子的物理属性(见式(1)).

1.3 多道次滚压

板料滚压成形属于“多工步法”，道次数、各道次路径及其角度均会影响板件塑性变形量的积累，从而影响板件的宏观成形质量和力学性能.多道次滚压本构关系的建立需要考虑中间卸载过程和不同硬化模型对滚压成形精度的影响，并由此确定多道次的工艺参数，即滚压的道次数、路径和角度，如图3所示.

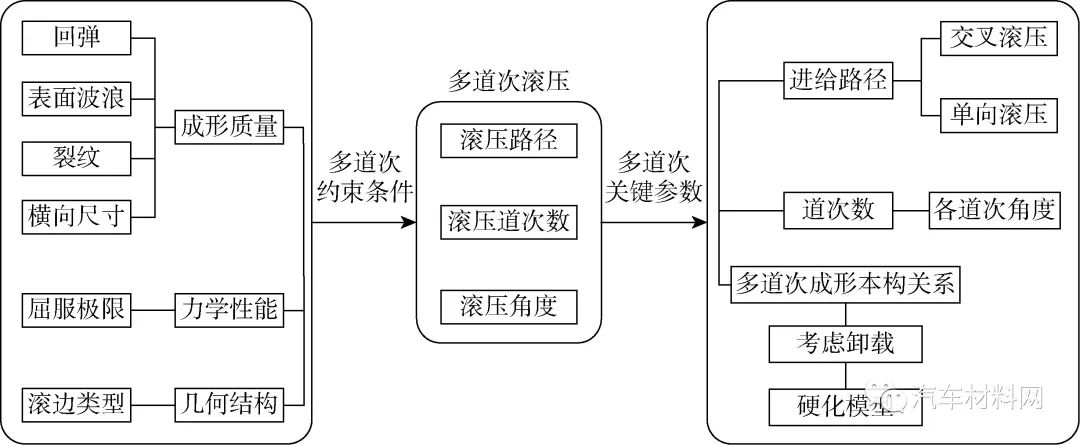
图3 多道次滚压特征分析

Fig.3 Feature analysis of multi-pass roll-hemming

2.1 滚压仿真建模

基于FEM-SPH进行滚压成形有限元仿真，以研究含胶铝板滚压变形规律.采用圆柱滚轮和圆锥滚轮双滚轮分别进行首道次和末道次滚压，滚压角度依次为45°和90°，几何模型如图4所示.其中，k1=0.8 mm和k2=1.0 mm分别为内、外板厚，e=5 mm为离边距，g=2 mm为内外板间距，W=104 mm 为胎模宽度，b=20 mm、d和d0分别为滚轮的宽度、直径和小径，H为翻边高度，R为圆角半径.此外，胎模长度为150 mm，滚轮锥度为45°，胶层直径为4 mm.

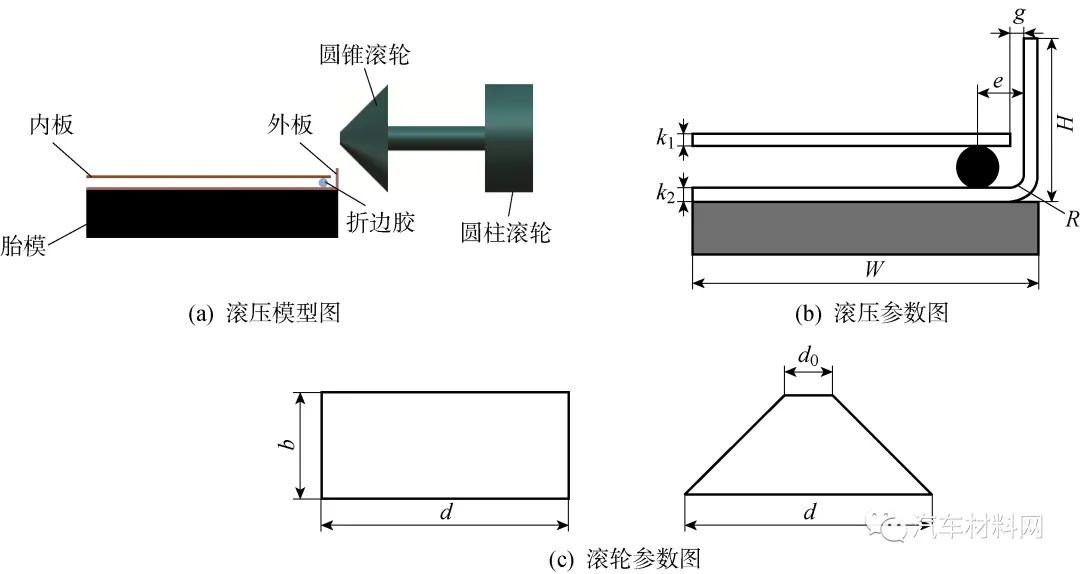
图4 滚压模型及滚轮结构参数

Fig.4 Roll-hemming model and roller structure parameters

铝外板材料选择铝合金AA6016-T4，其在汽车外覆盖件中应用广泛，化学成分组成和材料特性[12]如下：弹性模量70 GPa，密度2.7 g/cm3，泊松比0.3，屈服强度129 MPa，抗拉强度242 MPa，硬化指数(4%～6%)0.273，断裂伸长率26.9%.

折边胶选择陶氏BETAMATETM 240G(一种单组分环氧树脂结构胶)，常温下为红色糊状物，可在常温或30～60 ℃使用，密度为1.25 g/cm3(23 ℃)，弹性模量为 2 200 MPa，黏度为250 Pa·s (23 ℃)，屈服强度为560 Pa，断裂伸长率为0.04，固含量大于99%.

针对实际工艺中多道次滚压方式的复杂性问题，在仿真程序里设置多个分析步，模拟初始的压胶工艺和滚轮进给方式以及切换滚轮运动；利用SPH法将胶层转化为粒子，模拟胶层在滚压阶段发生的大变形.针对引入胶层导致的仿真时间变长和计算不收敛的现象，采用动态显示分析结合质量缩放方法，提升仿真速度的同时保障仿真精度.

2.1.1 多分析步设置 

进行滚压工序设计，设置压胶和滚轮进给路径，采用两道次交叉滚压进给方式.首先，内板下压3.8 mm，模拟压胶工艺，胶层由圆柱形胶条形式转变为流动状态填充内外板间隙.然后滚轮向外板方向进给，进行首道次滚压.最后双滚轮围绕中心旋转180°，完成圆锥滚轮向圆柱滚轮的切换，开始末道次滚压.在整个工艺过程中，不限制滚轮轴线方向的自由度，滚轮在与外板接触的过程中能够自由转动，如图5所示.

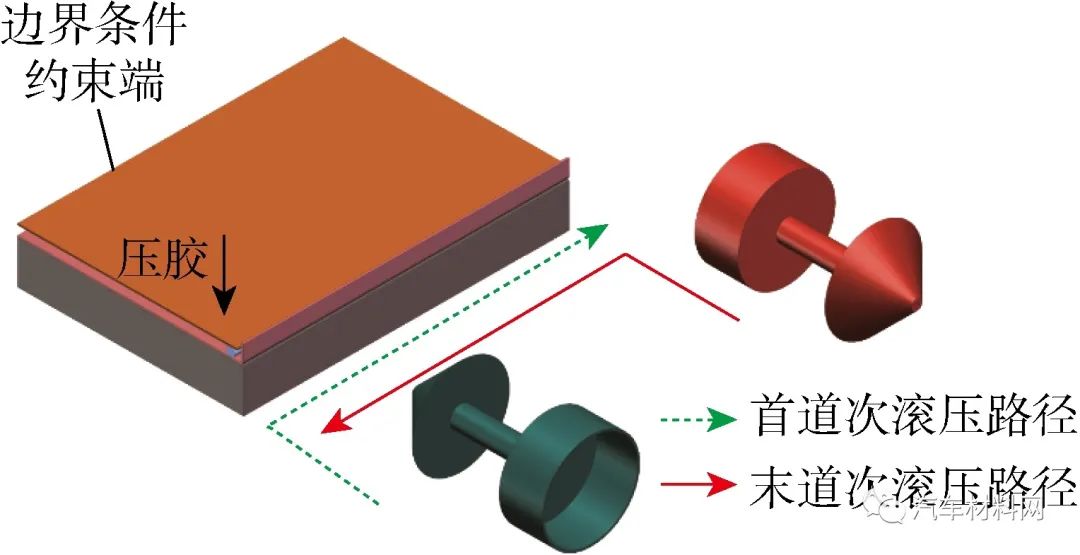
图5 压胶和滚轮进给方向

Fig.5 Pressure adhesive and roller feed direction

2.1.2 网格划分和SPH粒子转换 

所建滚压模型以六面体网格为主，支持网格单元直接转换为粒子，在外板折弯和滚压处网格较细密，其他位置按网格由疏到密的趋势单向划分，如图6所示.网格总数为 23 241，其中 21 500 个为C3D8R类型，1 703 个为R3D4类型，剩余为R3D3类型.

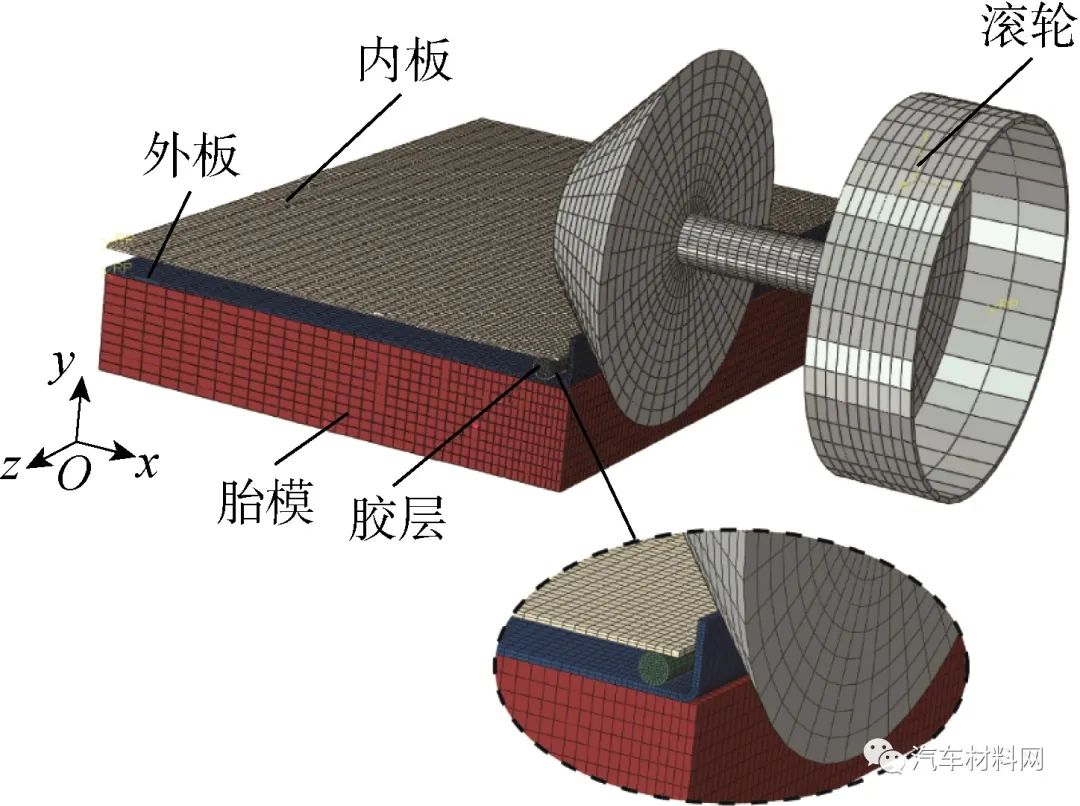
图6 网格划分

Fig.6 Mesh generation

2.2 滚压成形质量指标定义

滚压成形质量指标选择滚边损耗量(ε)和表面波浪系数(s).其中，ε值衡量滚压后外板边缘的横向尺寸变化，正值表示缩进，负值表示涨出，极大影响间隙面差.其测量方法为在滚压后外板边缘均匀取n个点，测量其到胎模边缘线的距离Li(i=1, 2, …，n)，如图7所示.计算公式如下：

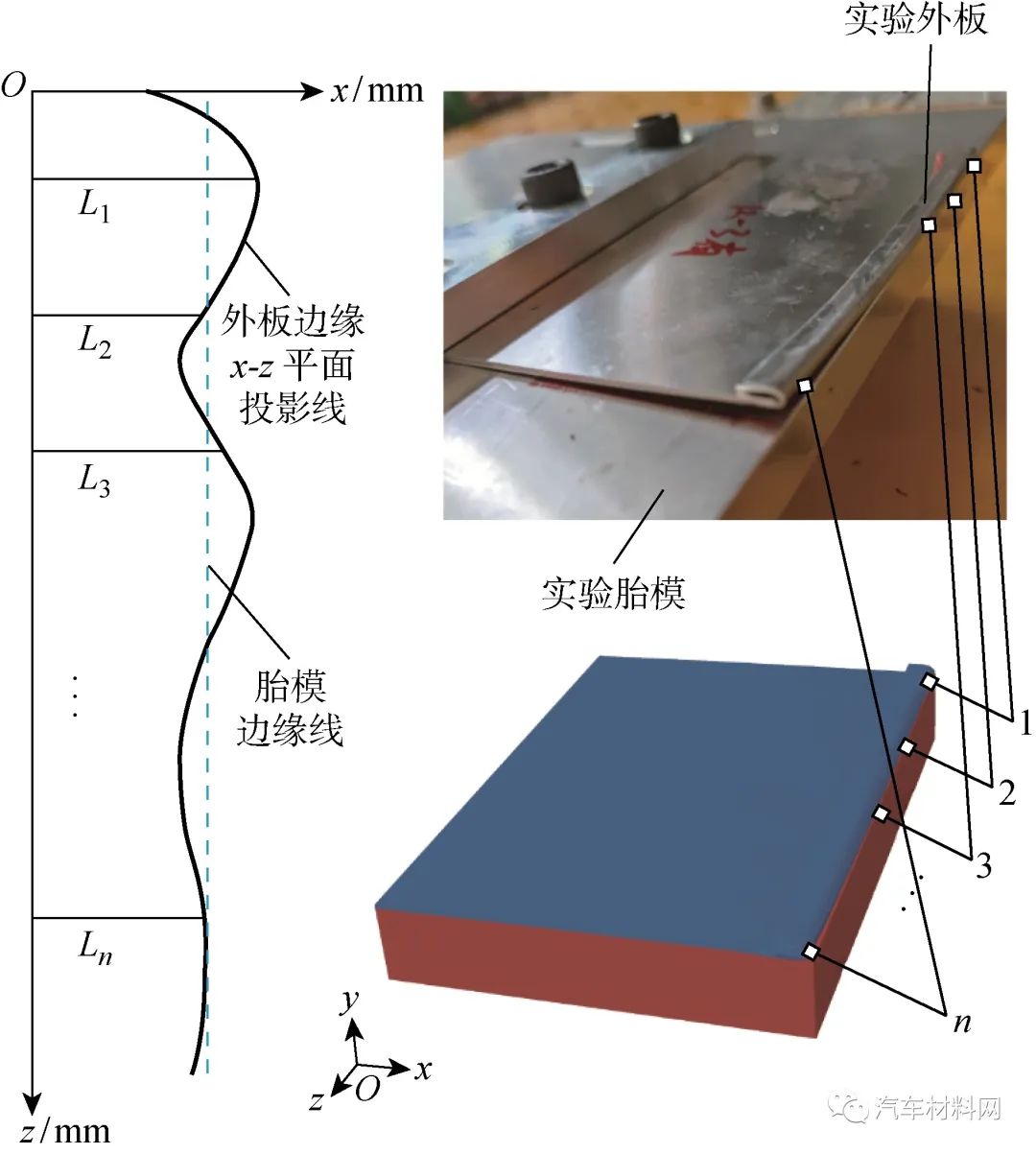
图7 滚边损耗量测量方法

Fig.7 Measurement method of roll-hemming loss

(3)

s值反映滚压后外板在翻边边缘处较大幅度的波浪起皱现象，极大影响车身外观和密封性能.其测量方法为在翻边边缘均匀取n个点，测量其到胎模面的距离hi(i=1, 2, …，n)，将hi值的变化幅度定义为波浪起皱程度，如图8所示.计算公式如下：

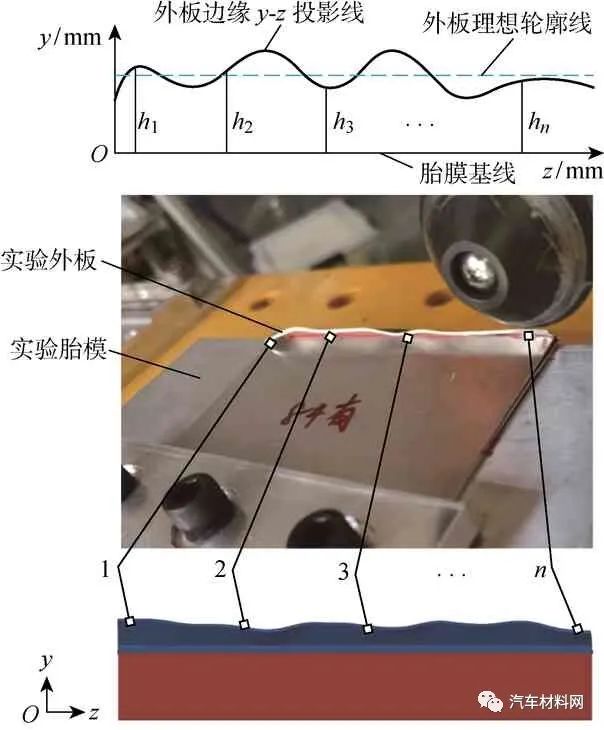
图8 表面波浪系数测量方法

Fig.8 Measurement method of surface wave coefficient

（4）

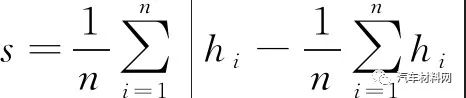
3.1 实验系统搭建

为验证仿真模型的有效性，搭建含胶铝板双滚轮滚压实验系统进行对比实验.所建滚压实验平台由机器人及其控制系统、滚压工具和夹具系统3部分组成，如图9所示.其中，滚压机器人为滚压工艺主体，其通过控制滚压工具的运动轨迹，按预设程序完成滚压操作.要求其具有较高的定位精度、负载能力和灵活度，因此选择KUKA机器人KR600 R2830.滚压工具为安装在机器人末端执行器上进行滚压操作的设备，选择圆柱滚轮与圆锥滚轮相结合的直轴双滚轮为滚压工具.夹具系统为将待滚压的车身薄板件进行定位和夹紧的装置，选择螺栓压紧块为夹紧方式，实验平台如图10所示.

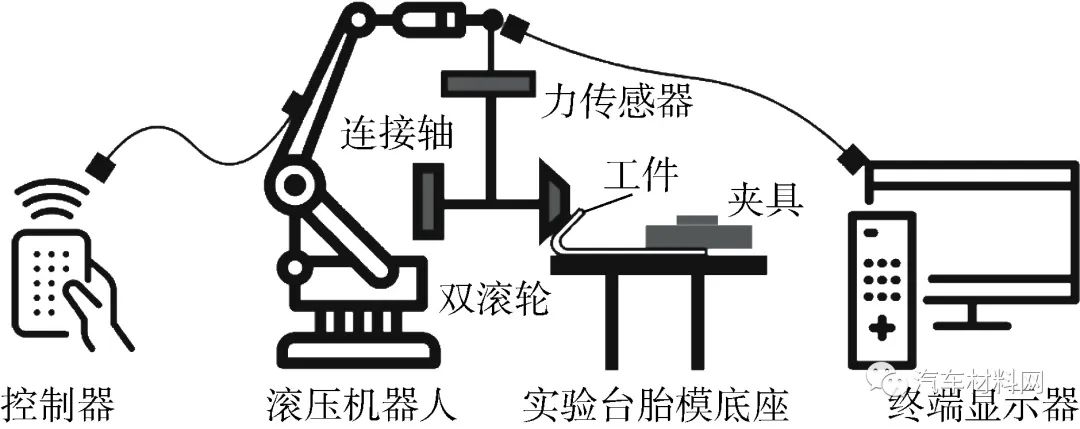
图9 滚压实验测量系统

Fig.9 Measurement system of roll-hemming experiment

图10 滚压实验系统

Fig.10 System of roll-hemming experiment

进行3组含胶滚压实验仿真对比，实验所用滚轮的直径均为70 mm，TCP-RTP值依次为L=1.5，2，2.5 mm，对应H=10，11，12 mm.此外，每组实验同时设置无胶对照组，以探究胶层对滚压成形质量的影响.

3.2 实验结果分析

双滚轮滚压实验过程如图11所示.初始阶段为准备阶段，在内外板之间涂敷一层陶氏折边胶BETAMATETM 240G，内板下压挤压胶层，用螺栓压紧块将含胶板材固定在胎模上；第2阶段为首道次滚压，使用圆锥滚轮；第3阶段为末道次滚压，机器人自由度和连接轴限制使得切换滚轮时连接轴向前进给；第4阶段为成形质量测量，选择多个点依次测量并计算出滚压工艺的成形质量指标值.

图11 多道次滚压实验步骤

Fig.11 Experiment passes of multi-pass roll-hemming

在外板边缘均匀取21个点，测量并计算滚边损耗量和表面波浪系数，各点测量结果如图12所示.实验测量结果如表1和表2所示.表2中，实验与仿真的两道次滚压成形质量值最大误差不大于11.9%，这可能是测量工具使用不当造成的.从对比结果来看，仿真方法可行， 精度可以保证.

表1 表面波浪系数对比

Tab.1 Comparison of surface wave coefficients

表2 滚边损耗量对比

Tab.2 Comparison of roll-hemming loss

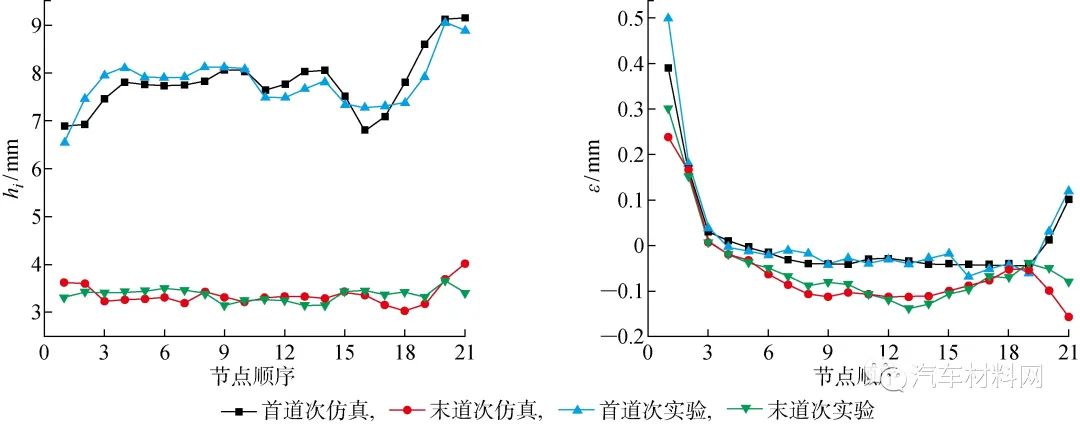
图12 测量结果对比

Fig.12 Comparison of measurement results

有胶和无胶的实验对比结果如图13所示.可知，相比于无胶滚边结构，有胶滚边结构的ε值和s值均有减小趋势，滚压质量得到提高.同时，无胶滚边结构两道次间的ε值和s值逐渐减小.

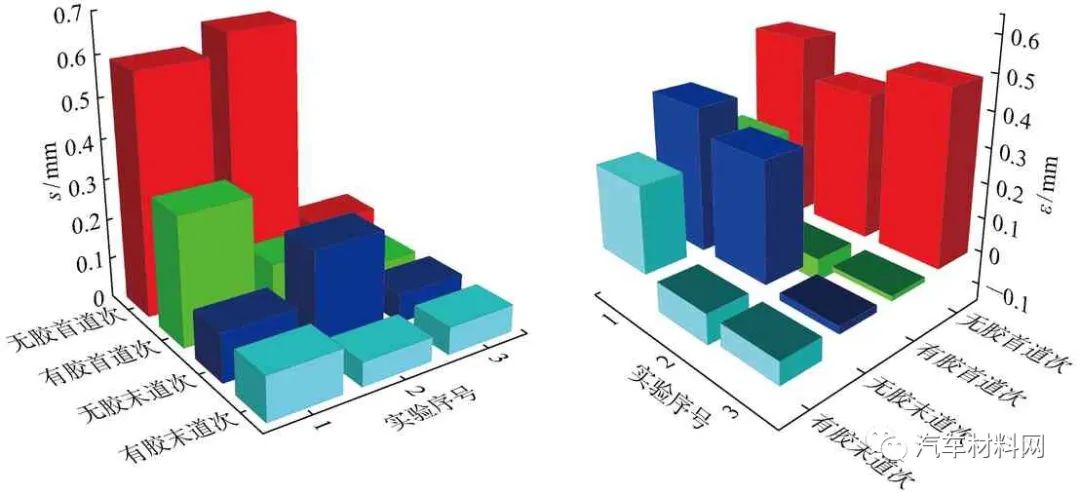
图13 胶层引入对滚压质量影响

Fig.13 Influence of adhesive on roll-hemming quality

4.1 工艺参数影响

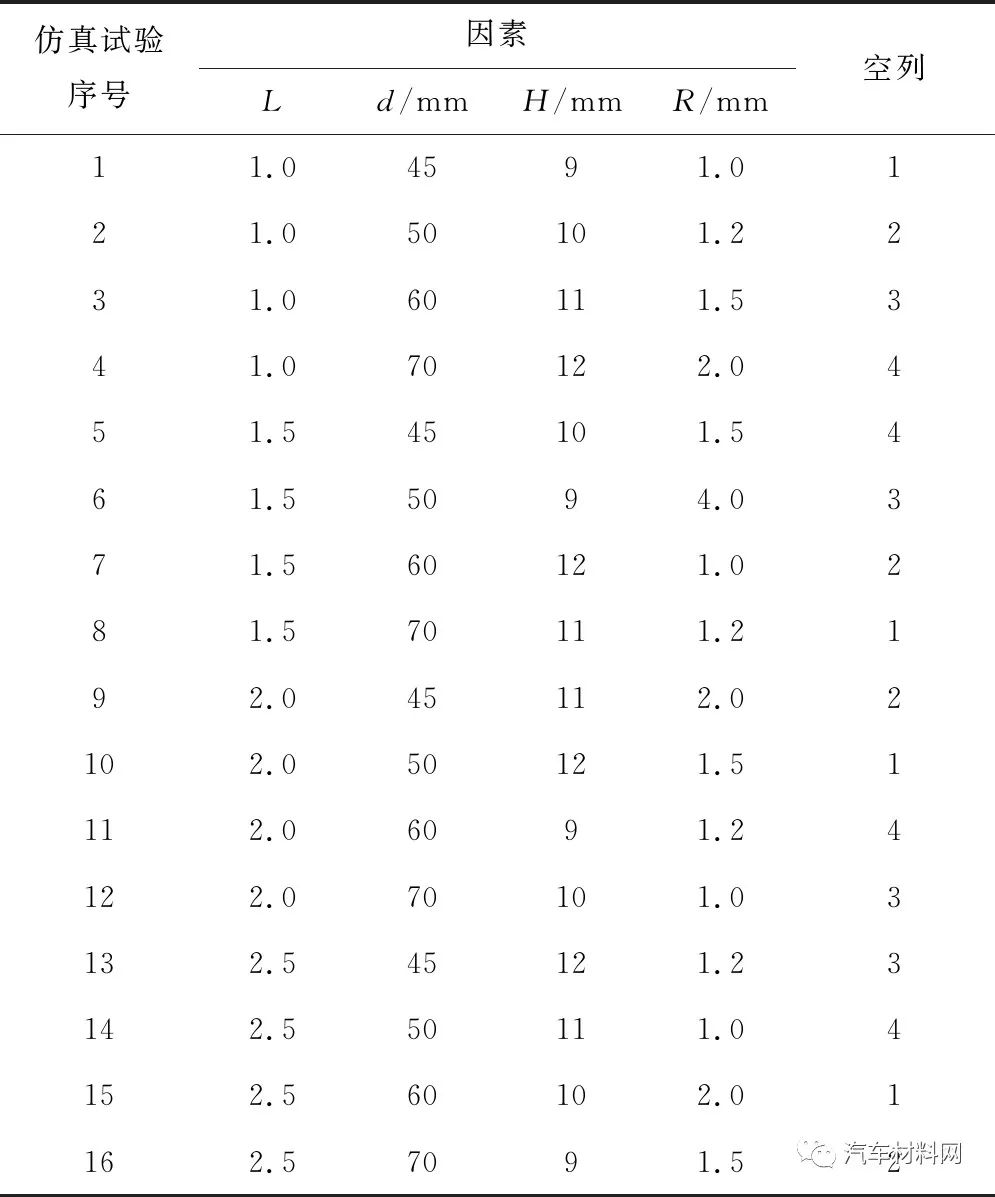
在薄板滚压中，工艺参数对滚压成形质量有很大影响.在验证仿真模型的有效性后，进一步研究关键工艺参数对滚压质量的影响.采用正交试验法进行多因素仿真试验，如表3所示.仿真结束后，在外板边缘和滚压处分别均匀取21个点，删去首尾两端点和误差较大的异常点，测量并计算ε值和s值.

表3 L16(45)正交试验表

Tab.3 Orthogonal test schedule of L16(45)

为了研究两道次滚压首末道次之间的关系，分别测量首道次和末道次的ε值和s值.图14为仿真试验8的两道次波浪系数对比.其中，τ为Mises应力.可知，对于两道次滚压，首道次滚压后的表面波浪程度较大，其s值与末道次滚压相比较大.

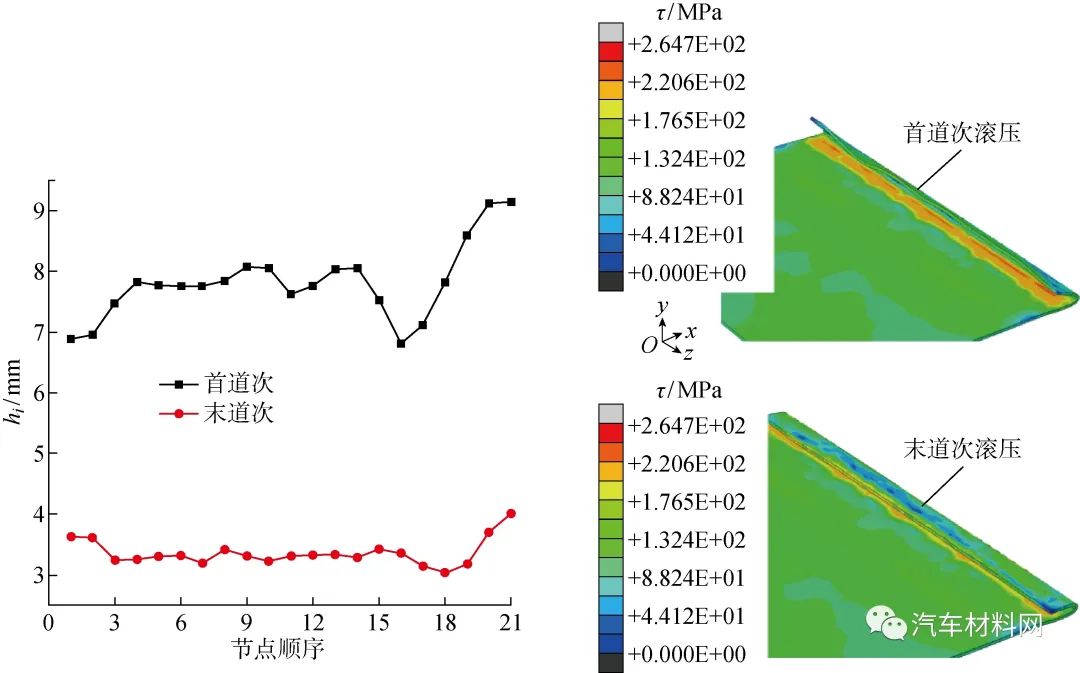
图14 两道次滚压波浪系数对比

Fig.14 Wave coefficients of roll-hemming in two passes

图15为仿真试验10的两道次滚边损耗量对比.可知，对于两道次滚压，与首道次滚压完成时相比，末道次滚压的ε值较小，即缩进值较小.在末道次滚压过程中，外板边缘受到滚轮的挤压力作用而产生向外扩展的趋势，横向尺寸变大.

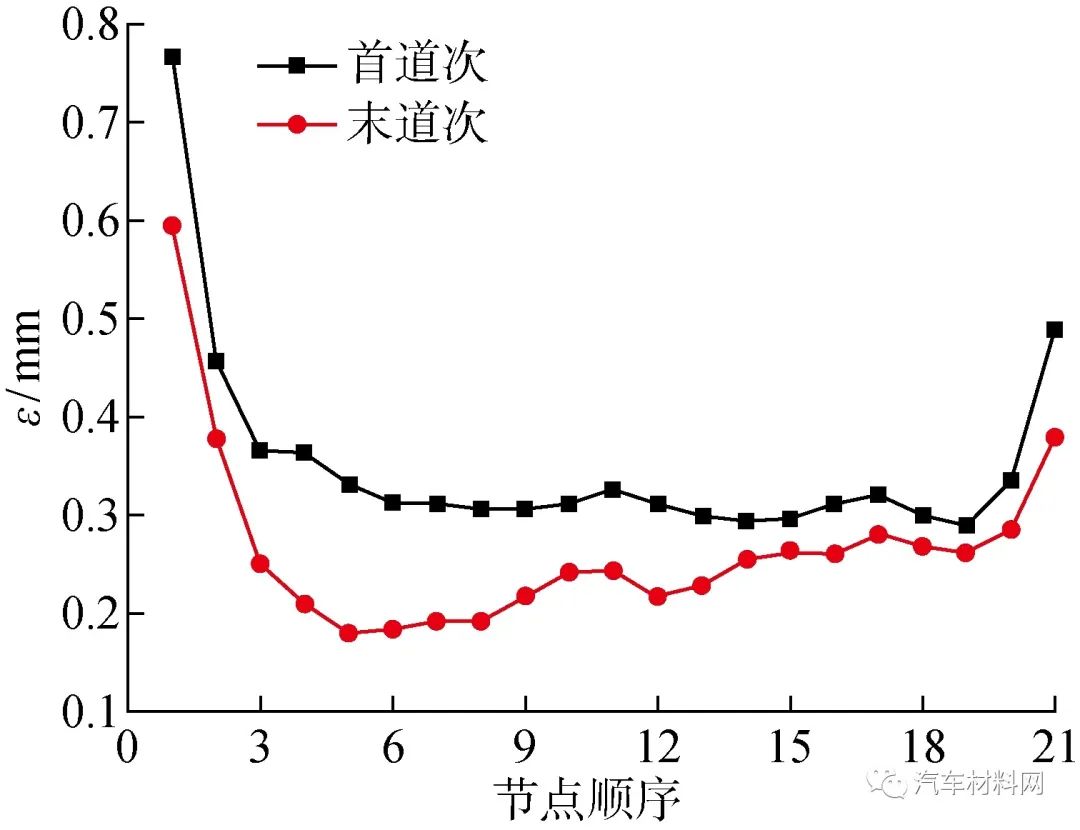
图15 两道次滚压滚边损耗量对比

Fig.15 Roll-hemming loss of roll-hemming in two passes

图16为正交仿真试验两道次滚压质量指标变化趋势.可知，除个别数据点外， 每一组仿真数据的变化趋势相同：与首道次滚压相比，末道次滚压的ε值和s值均较小，横向尺寸有增大趋势.

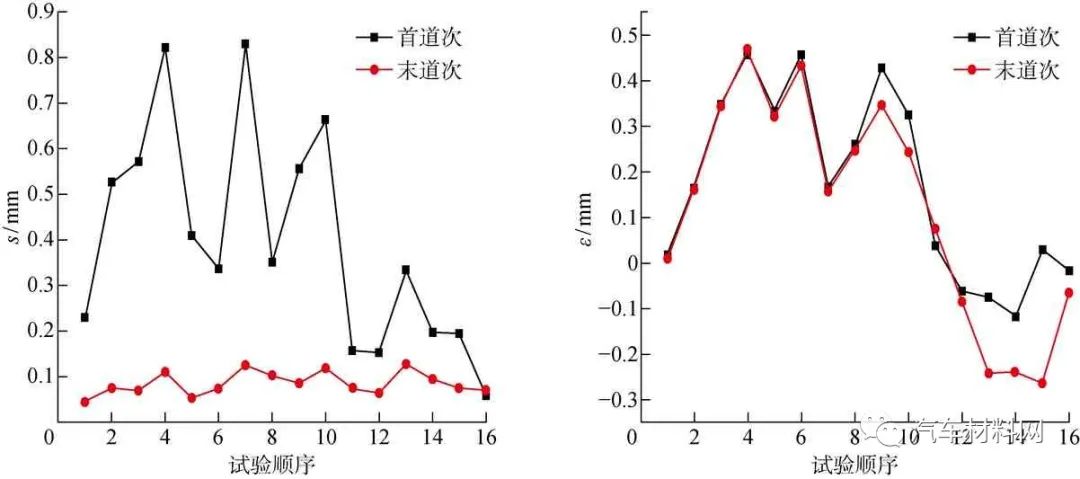
图16 两道次滚压成形质量指标变化趋势

Fig.16 Quality index of roll-hemming forming in two passes

对正交试验仿真结果进行方差分析，结果如表4所示.其中，F为检验统计量，Fa为F分布分位数.可知，在对s值的影响程度方面，H值最显著，L值和R值次之，d值最小；在对ε值的影响程度方面，L值最显著，R值次之，d值和H值最小.

表4 影响因素方差分析

Tab.4 Analysis of variance of influencing factors

翻边高度和TCP-RTP值对两个质量指标的影响程度较大，对其进行单因素分析，如图17所示.每个工艺参数的取值均为4组，可进行综合对比研究.可知，在9～12 mm范围内，随H值增大，s值逐渐增大，则波浪起皱程度逐渐增加；在1～2.5 mm范围内，随L值增大，ε值逐渐减小，则外板边缘横向尺寸增大.

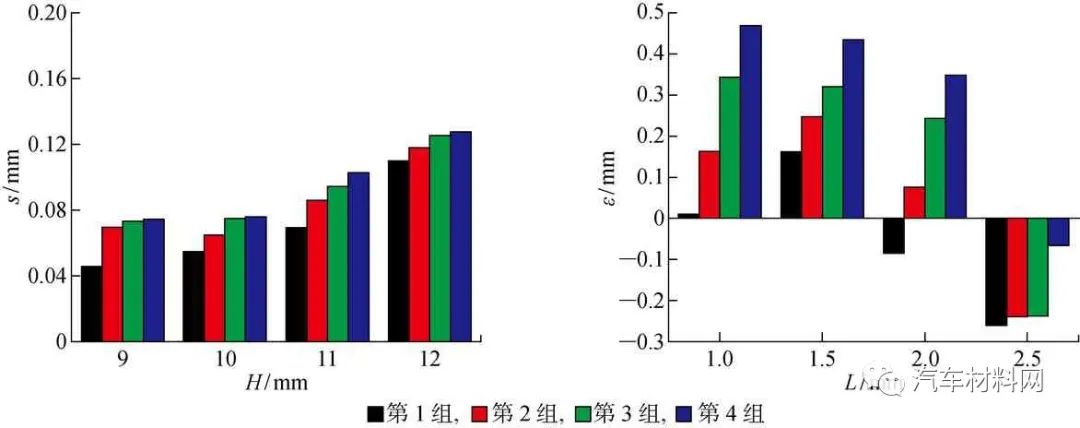
图17 滚压成形质量指标单因素影响分析

Fig.17 Analysis of single factor of roll-hemming forming quality index

4.2 含胶铝合金薄板滚压成形质量预测

为准确预测含胶薄板的滚压成形质量，利用多元拟合函数对上述仿真数据进行多变量拟合，探究滚压质量指标与工艺参数之间的定量关系，得到的拟合关系如下：

ε=0.184 2-0.033 4L3+6.83×10-8d3+4.7×10-5H3+0.026 9R3, R2=0.89

(5)s=-0.114 5-0.018 8L-1.53×109-0.052 4d-4.72+4.09×10-9H6.72+0.177 6R-0.1, R2=0.94

(6)利用式(5)和式(6)可以预测特定工艺参数条件下的含胶铝板滚压成形质量，为实际生产中的滚压质量控制优化提供参考.

(1) 提出一种基于FEM-SPH的含胶薄板滚压成形分析模型，并利用双滚轮滚压对比实验证明了所建滚压仿真分析模型的有效性.

(2) 与首道次滚压相比，末道次滚压的ε值和s值均较小，滚压工艺成形质量较好；与无胶相比，引入胶层后的ε值和s值均具有降低趋势.翻边高度对s值的影响显著，翻边高度增加，s值随之增大；TCP-RTP值对ε值的影响显著，TCP-RTP值增大，ε值随之减小.

(3) 构建滚压成形质量指标与工艺参数之间的拟合关系式，进行含胶铝合金薄板滚压成形质量预测.

(4) 该含胶薄板滚压成形分析方法所采用的平面直边滚边结构较简单，后续将进一步深入研究不同滚边结构和胶层厚度等参数对滚压工艺的影响.

参考文献：

[1] LIMON-LEYVA P A, BALVANTN A J, DIOSDADO-DE-LA-PEA J A, et al. Parametric optimization of roll-hemming process in oblique planes with linear and non-linear trajectories[J]. Journal of Manufacturing Processes, 2020, 50: 123-131.

[2] 韩飞, 李荣健. 超高强钢多道次辊弯成形回弹规律研究[J].机械工程学报, 2019, 55(2): 73-81.

HAN Fei, LI Rongjian. Springback law of ultra high strength steel in multiple stands roll forming process[J]. Journal of Mechanical Engineering, 2019, 55(2): 73-81.

[3] 李雪龙, 于忠奇, 赵亦希, 等. 多道次普旋预成形阶段法兰起皱预测[J]. 上海交通大学学报, 2019, 53(11): 1375-1380.

LI Xuelong, YU Zhongqi, ZHAO Yixi, et al. Study on flange wrinkling prediction in preforming stage during multi-pass conventional spinning[J]. Journal of Shanghai Jiao Tong University, 2019, 53(11): 1375-1380.

[4] LE MAOT N, MANACH P Y, THUILLIER S. Influence of prestrain on the numerical simulation of the roller hemming process[J]. Journal of Materials Processing Technology, 2012, 212(2): 450-457.

[5] HU X, LIN Z Q, LI S H, et al. Fracture limit prediction for roller hemming of aluminum alloy sheet[J]. Materials & Design, 2010, 31(3): 1410-1416.

[6] 程楠.水滴包边技术在汽车发动机罩盖上的应用[J].汽车工艺与材料, 2016(1): 11-13.

CHENG Nan. Application of water drop wrapping technology on automobile hood hood[J]. Automobile Technology & Material, 2016(1): 11-13.

[7] 肖寿仁, 李军, 周燕辉. 汽车车顶天窗成形工艺及翻边回弹补偿分析[J]. 热加工工艺, 2012, 41(5): 80-83.

XIAO Shouren, LI Jun, ZHOU Yanhui. Flange forming process of car sunroof skylight and its springback compensation analysis[J]. Hot Working Technology, 2012, 41(5): 80-83.

[8] 郭婷婷. 汽车天窗滚边工艺仿真分析及实验研究[D].合肥: 合肥工业大学, 2016.

GUO Tingting. The simulation analysis and experimental study of the sunroof roller hemming[D]. Hefei: Hefei University of Technology, 2016.

[9] KLEEH T, MERKLEIN M, ROLL K. Modeling laser heating for roller hemming applications[J]. Key Engineering Materials, 2011, 473: 501-508.

[10] 余魁, 赵顺旺, 柳玉起. 优化滚边工艺提升车门区域尺寸匹配精度的方法研究[J]. 精密成形工程, 2019, 11(3): 122-126.

YU Kui, ZHAO Shunwang, LIU Yuqi. Dimensional accuracy on matching areas of vehicle doors by optimizing hemming process[J]. Journal of Netshape Forming Engineering, 2019, 11(3): 122-126.

[11] 李萍, 井碧臣, 黄彪, 等. 1100铝合金双滚轮滚压包边模拟及实验研究[J]. 精密成形工程, 2018, 10(2): 92-98.

LI Ping, JING Bichen, HUANG Biao, et al. Simulation and experimental study on double-roller rolling hemming process of 1100 aluminum alloy[J]. Journal of Netshape Forming Engineering, 2018, 10(2): 92-98.

[12] LIEWALD M, HÖNLE S, SINDEL M. Surface roughening of an aluminum 6016 alloy during bending and hemming[J]. International Journal of Material Forming, 2016, 9(2): 203-213.

[13] 伍俊棠, 赵亦希, 李淑慧, 等. 滚压包边角度对包边件轮廓尺寸变动的影响[J]. 锻压技术, 2010, 35(3): 29-33.

WU Juntang, ZHAO Yixi, LI Shuhui, et al. Effect of hemming angle on dimensional deviation during roller hemming process[J]. Forging & Stamping Technology, 2010, 35(3): 29-33.

[14] 卢鹏, 兰凤崇, 周云郊. 机器人铝合金滚边参数对其质量影响的研究[J]. 机械设计与制造, 2015(9): 101-103.

LU Peng, LAN Fengchong, ZHOU Yunjiao. Study on quality influence of roller hemming parameters about aluminum alloy roller hemming parameters by robot[J]. Machinery Design & Manufacture, 2015(9): 101-103.

[15] 张均华, 刘渝, 杨睿, 等. 滚压包边成形质量缺陷研究[J]. 制造业自动化, 2015, 37(6): 26-28.

ZHANG Junhua, LIU Yu, YANG Rui, et al. The research of quality defect of robot roller hemming[J]. Manufacturing Automation, 2015, 37(6): 26-28.

[16] 卢妍, 张宁红, 陈中春, 等. 汽车开启件滚边工艺缺陷控制方法研究[J]. 模具技术, 2015(4): 1-4.

LU Yan, ZHANG Ninghong, CHEN Zhongchun, et al. Research on defect control methods for robotic roller hemming process of autobody components[J]. Die and Mould Technology, 2015(4): 1-4.

[17] 李建军, 朱文峰.基于SPH的平面曲线铝合金薄板滚压成形数值仿真与试验研究[J]. 机械工程学报, 2020, 56(24): 61-71.

LI Jianjun, ZHU Wenfeng. Numerical simulation and experiment of roller hemming-compression with flat surface-curved edge aluminum alloy sheet based on SPH[J]. Journal of Mechanical Engineering, 2020, 56(24): 61-71.

[18] 徐文欢. 车身覆盖件用折边胶涂覆质量问题分析及控制措施[J]. 汽车工艺与材料, 2019(3): 9-13.

XU Wenhuan. Quality problem analysis and control measures of hemming adhesive coating for automotive body panel[J]. Automobile Technology & Material, 2019(3): 9-13.

[19] MOBARA S E H, GHOBADIAN R, ROUZBAHANI F, et al. Numerical simulation of non-rigid landslide into reservoir with erodible sediment bed using SPH method[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(6): 4347-4366.