







Shift-Share工具变量的基本思想,是将一个宏观层面的“冲击”与一个微观单元的“初始份额”相结合,构造出一个随个体变化的工具变量。其经典形式可以表达为:
工具变量 = Σ(个体在某个维度上的初始份额 × 更高维度上的宏观冲击强度)这种方法的核心逻辑在于,它模拟了一种“差异性暴露”机制:不同的个体(如地区、企业),由于其初始结构不同,即使面对相同的宏观冲击,受到的影响强度也各异。这种差异化的影响,为识别因果关系提供了可能。
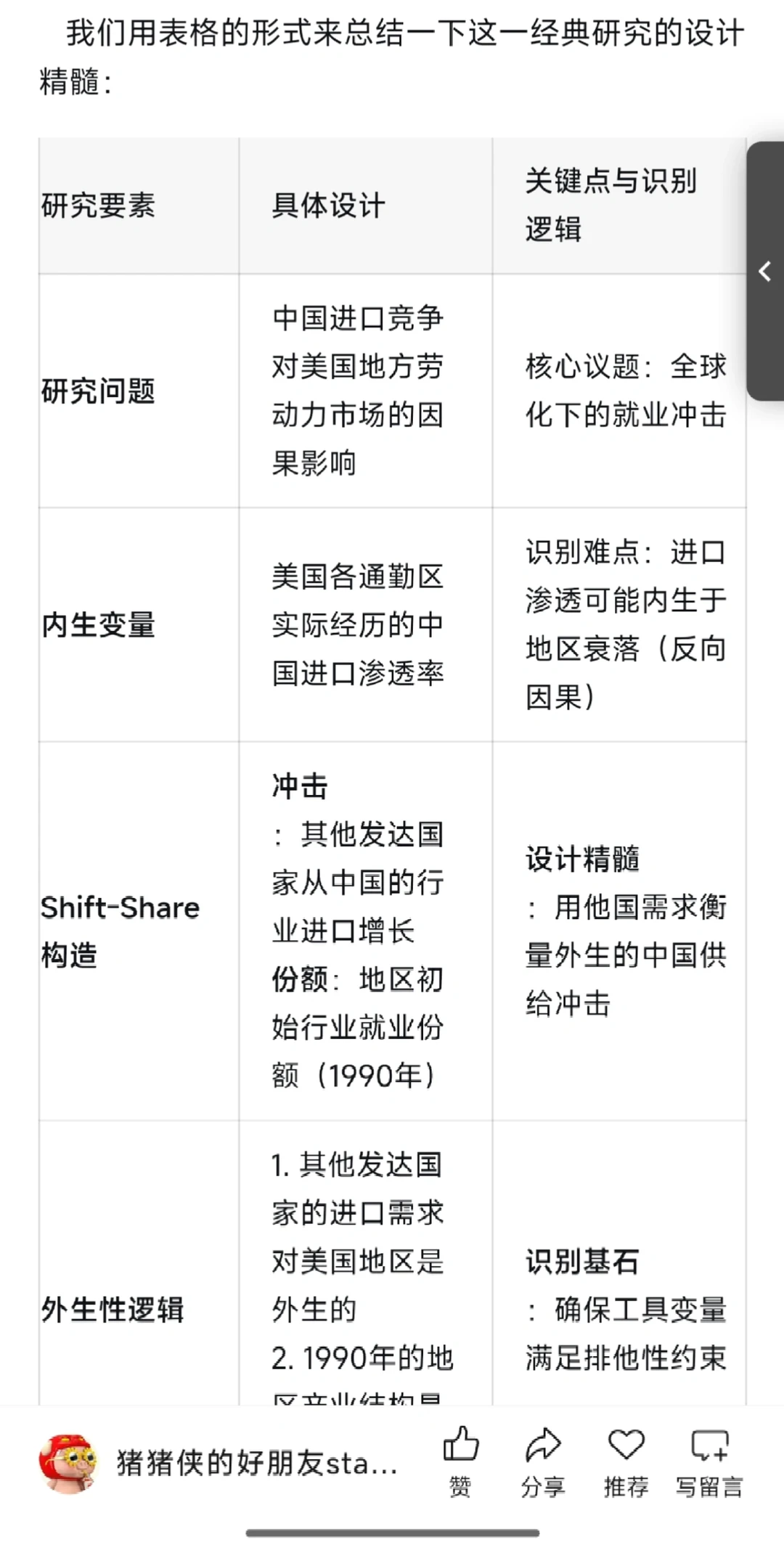
2013年,Autor等发表了一篇开创性论文,研究中国进口竞争对美国地方劳动力市场的影响。他们面临的挑战是:从中国进口的增加,可能内生于美国某些地区的经济衰退。
因此,他们的解决方案是构建一个Shift-Share工具变量:
冲击:其他发达国家(如欧盟国家)从中国的进口增长。这捕捉了中国的全球供给能力提升,对美国特定地区而言是外生的。
份额:美国各“通勤区”在1990年(早于中国冲击全面到来)的行业就业构成。
构造:将每个通勤区1990年的行业就业份额乘以相应行业在其他发达国家的进口增长,得到一个对该地区“潜在进口竞争压力”的测度。
这一设计巧妙地分离了外生的中国供给冲击与美国本土需求变化,最终发现中国的进口竞争显著降低了美国受影响地区的就业率。
#stata #论文 #实证分析 #计量经济学 #工具变量#stata实证 #Bartik工具变量 #移动份额工具变量 #工具变量法 #工具变量回归
工具变量 = Σ(个体在某个维度上的初始份额 × 更高维度上的宏观冲击强度)这种方法的核心逻辑在于,它模拟了一种“差异性暴露”机制:不同的个体(如地区、企业),由于其初始结构不同,即使面对相同的宏观冲击,受到的影响强度也各异。这种差异化的影响,为识别因果关系提供了可能。
2013年,Autor等发表了一篇开创性论文,研究中国进口竞争对美国地方劳动力市场的影响。他们面临的挑战是:从中国进口的增加,可能内生于美国某些地区的经济衰退。
因此,他们的解决方案是构建一个Shift-Share工具变量:
冲击:其他发达国家(如欧盟国家)从中国的进口增长。这捕捉了中国的全球供给能力提升,对美国特定地区而言是外生的。
份额:美国各“通勤区”在1990年(早于中国冲击全面到来)的行业就业构成。
构造:将每个通勤区1990年的行业就业份额乘以相应行业在其他发达国家的进口增长,得到一个对该地区“潜在进口竞争压力”的测度。
这一设计巧妙地分离了外生的中国供给冲击与美国本土需求变化,最终发现中国的进口竞争显著降低了美国受影响地区的就业率。
#stata #论文 #实证分析 #计量经济学 #工具变量#stata实证 #Bartik工具变量 #移动份额工具变量 #工具变量法 #工具变量回归


