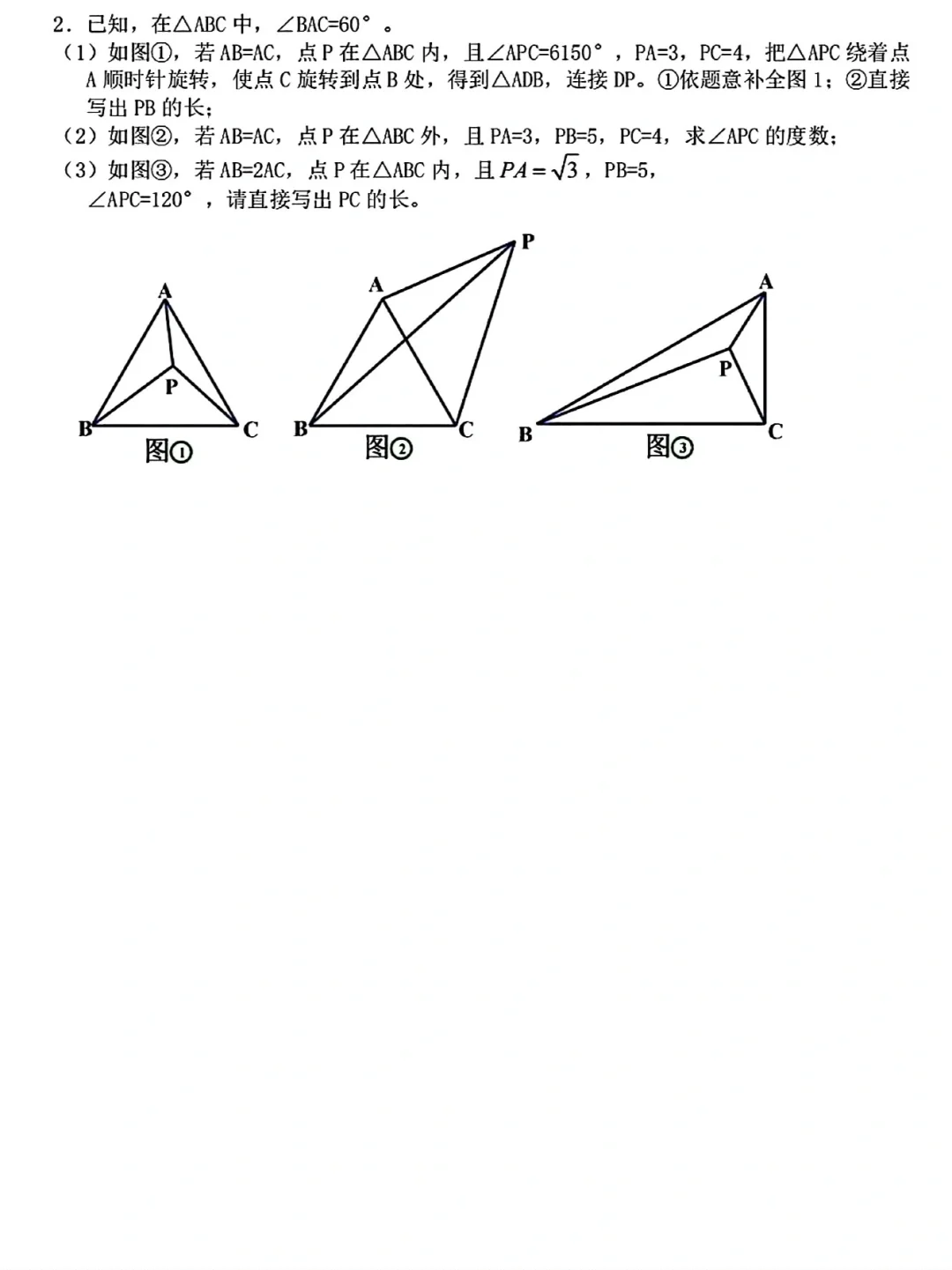
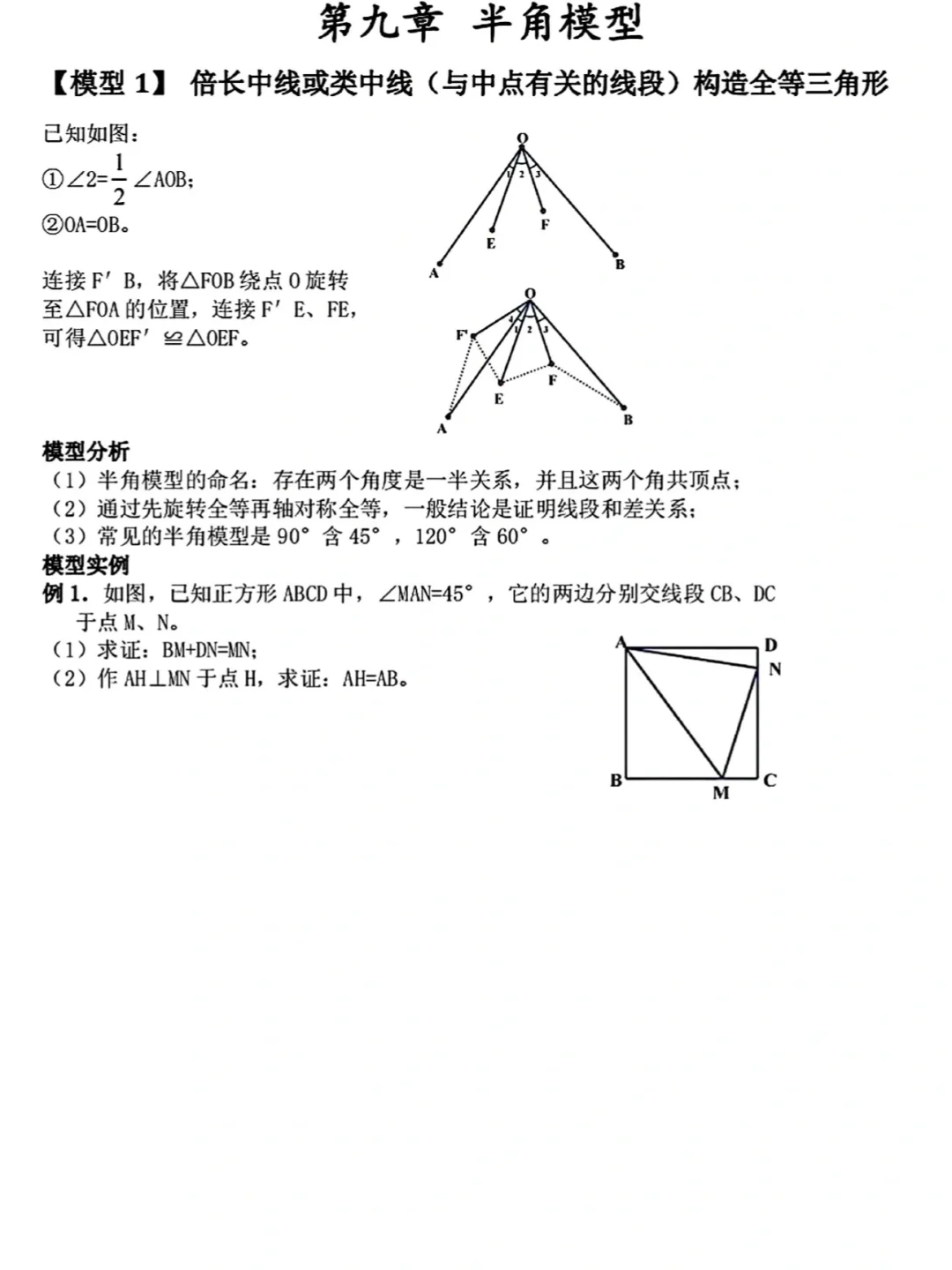
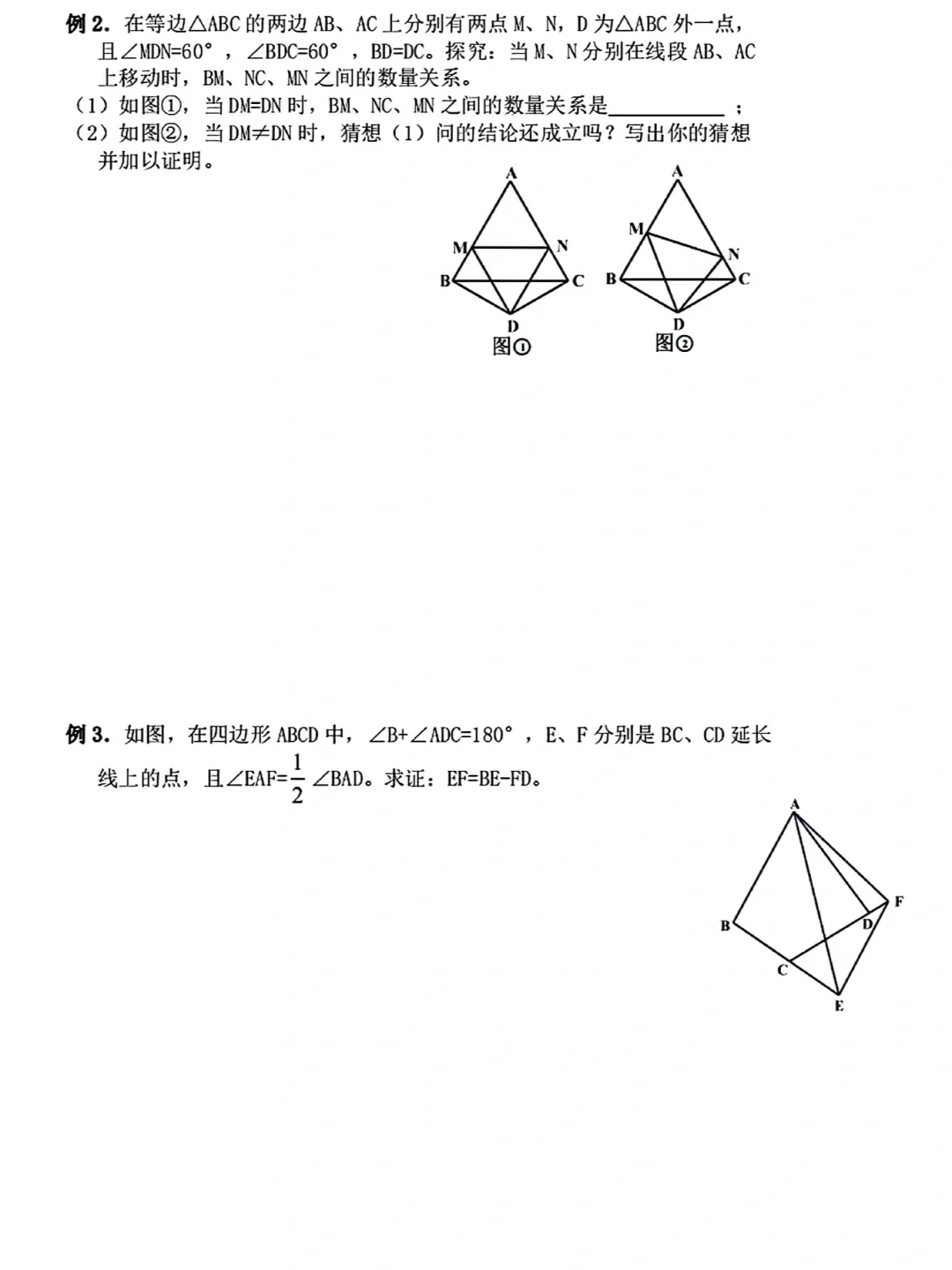
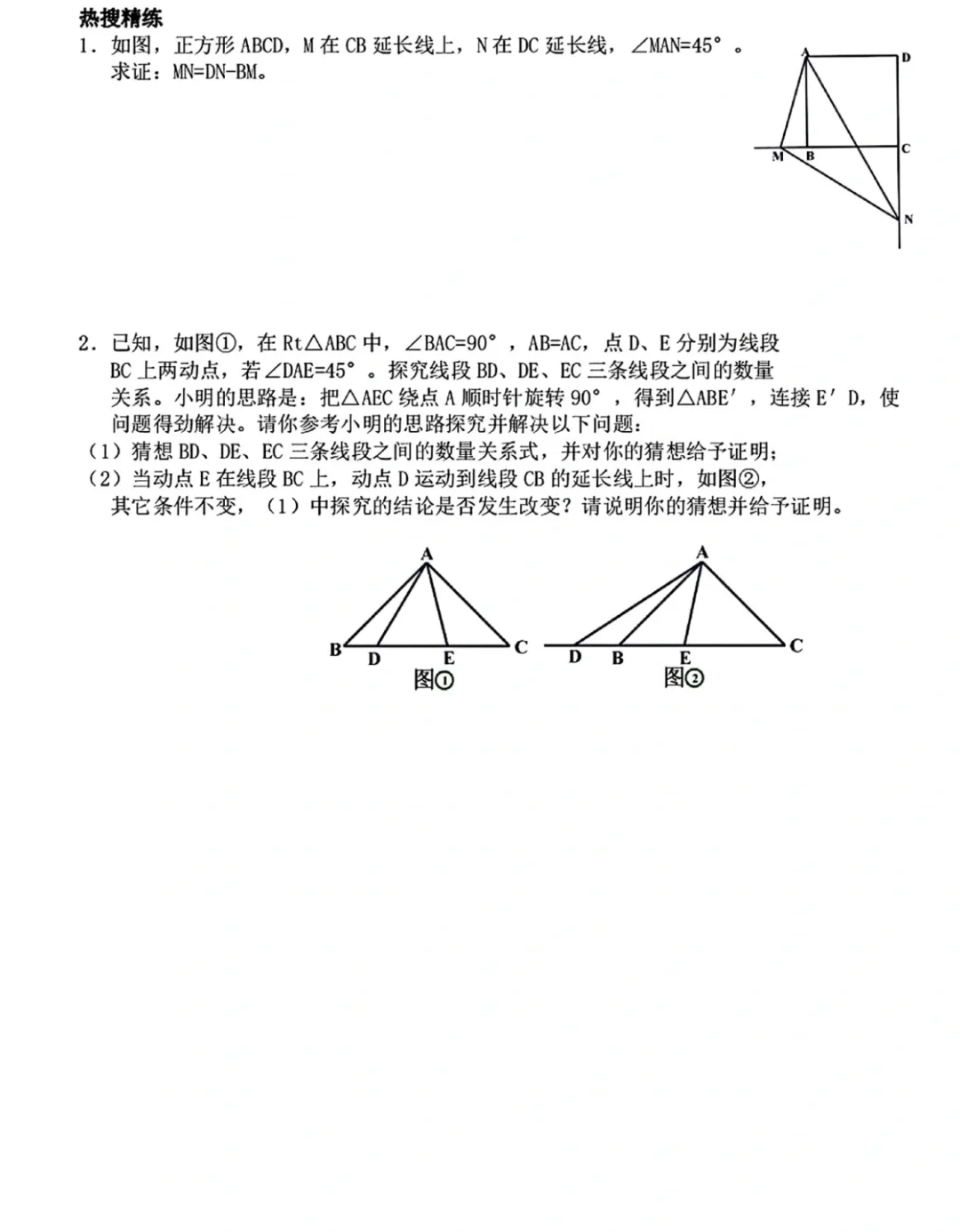

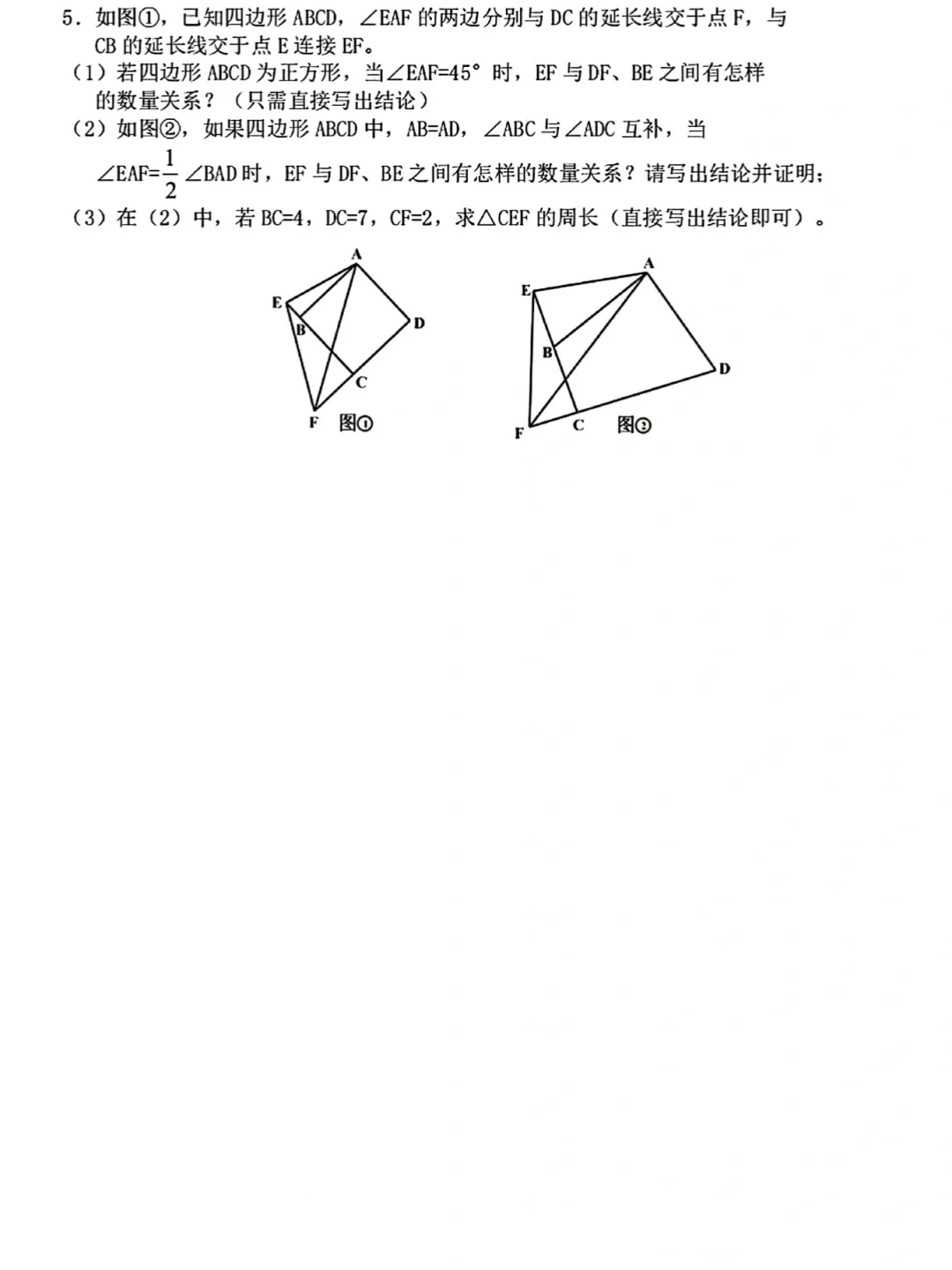


半角模型是指在一个角的内部有一个度数是它一半的角,由此构成的几何模型,核心是通过旋转构造全等三角形,实现线段或角的转化。
最典型的是“90°含45°”模型(如正方形中)和“120°含60°”模型(如等边三角形中),解题思路高度统一:
1. 旋转构造:将半角旁边的一个三角形绕顶点旋转,使与半角相关的两条相等线段重合。
2. 证明全等:旋转后,新形成的三角形与半角另一侧的三角形全等(通常用SAS判定)。
3. 推导结论:利用全等得到线段相等或角相等,进而推导出最终结论(如线段和差、角度关系等)。
初中阶段最核心的四大相似模型如下:
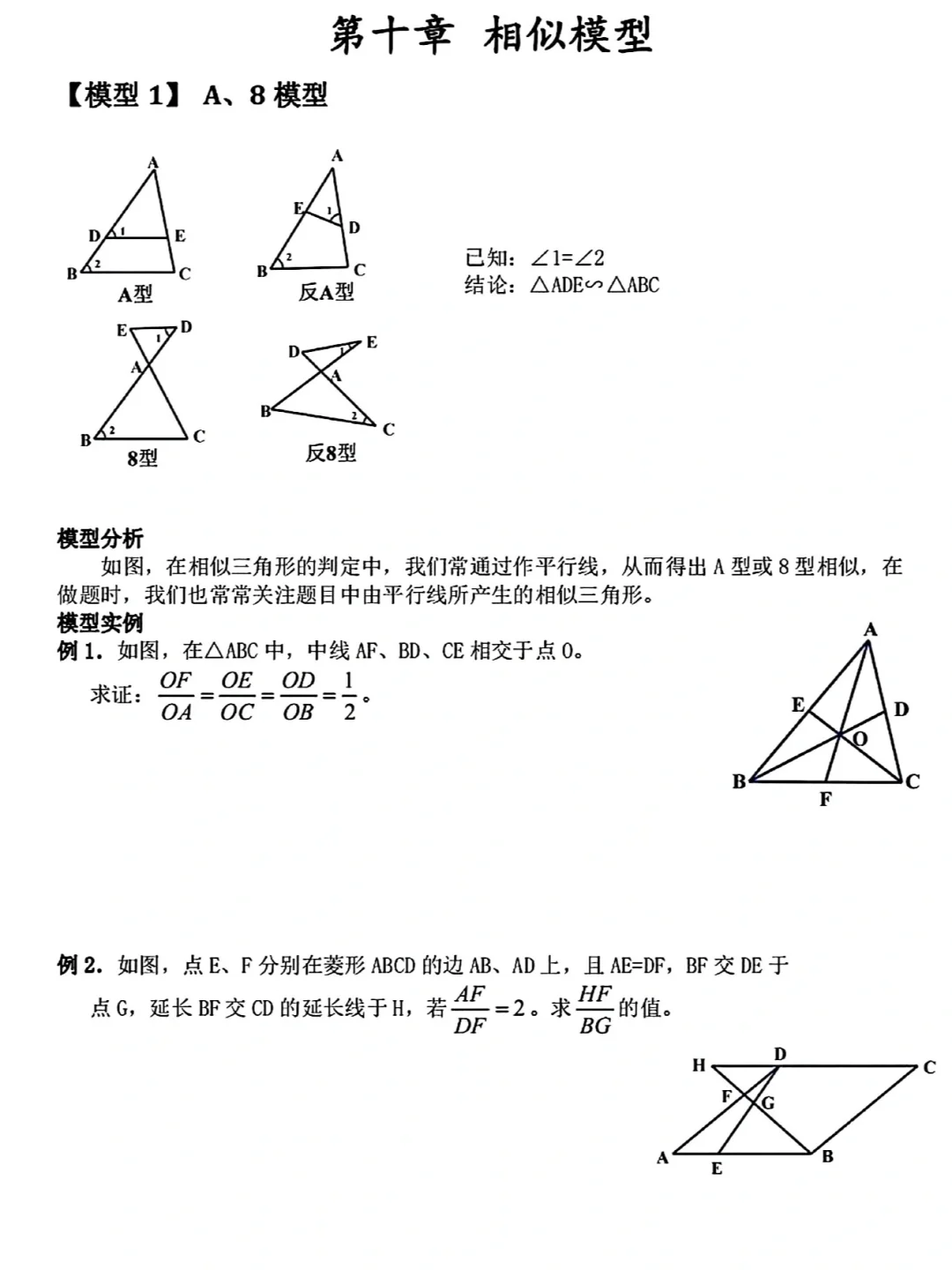
• A字型(含反A字型):
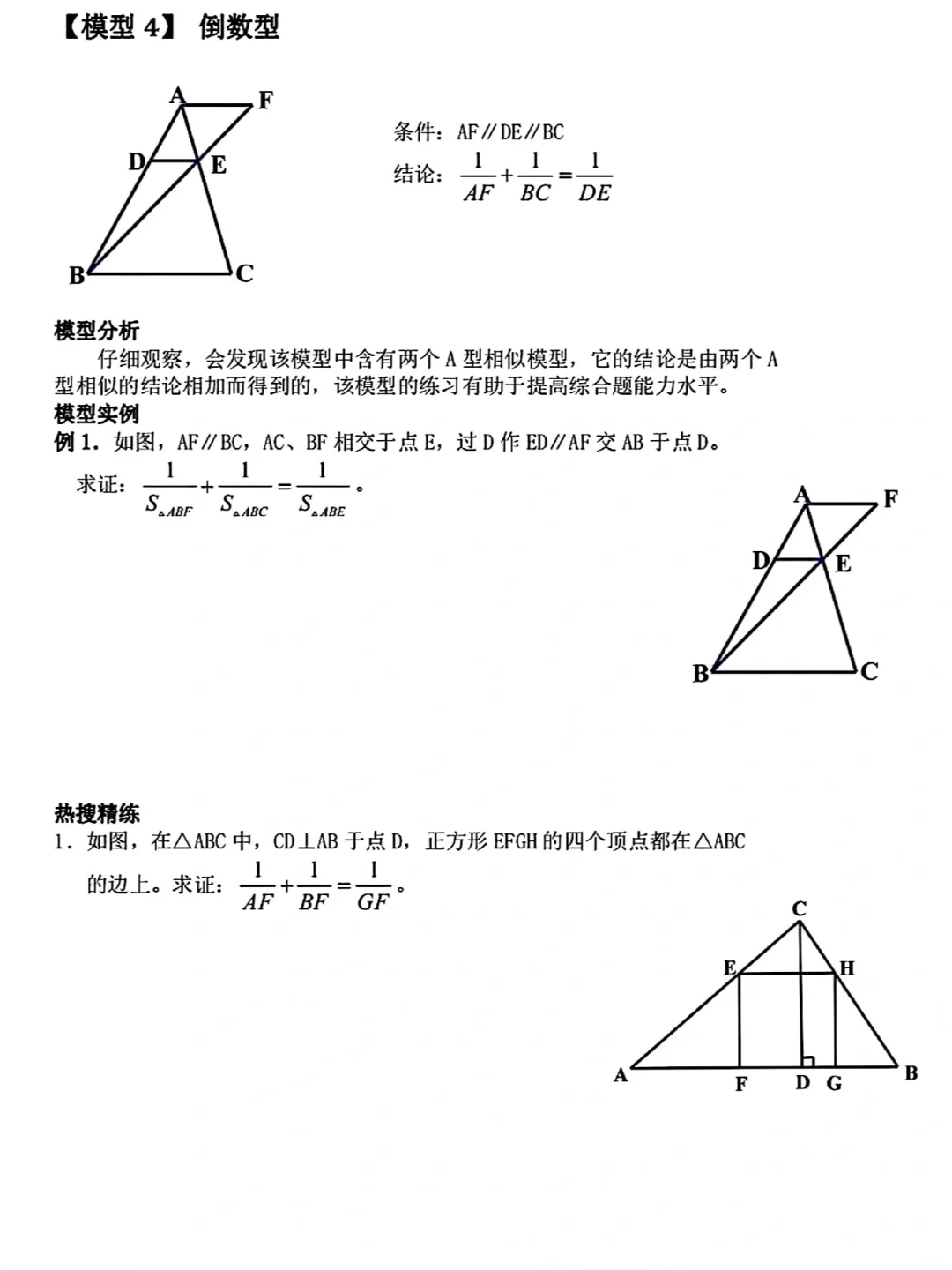
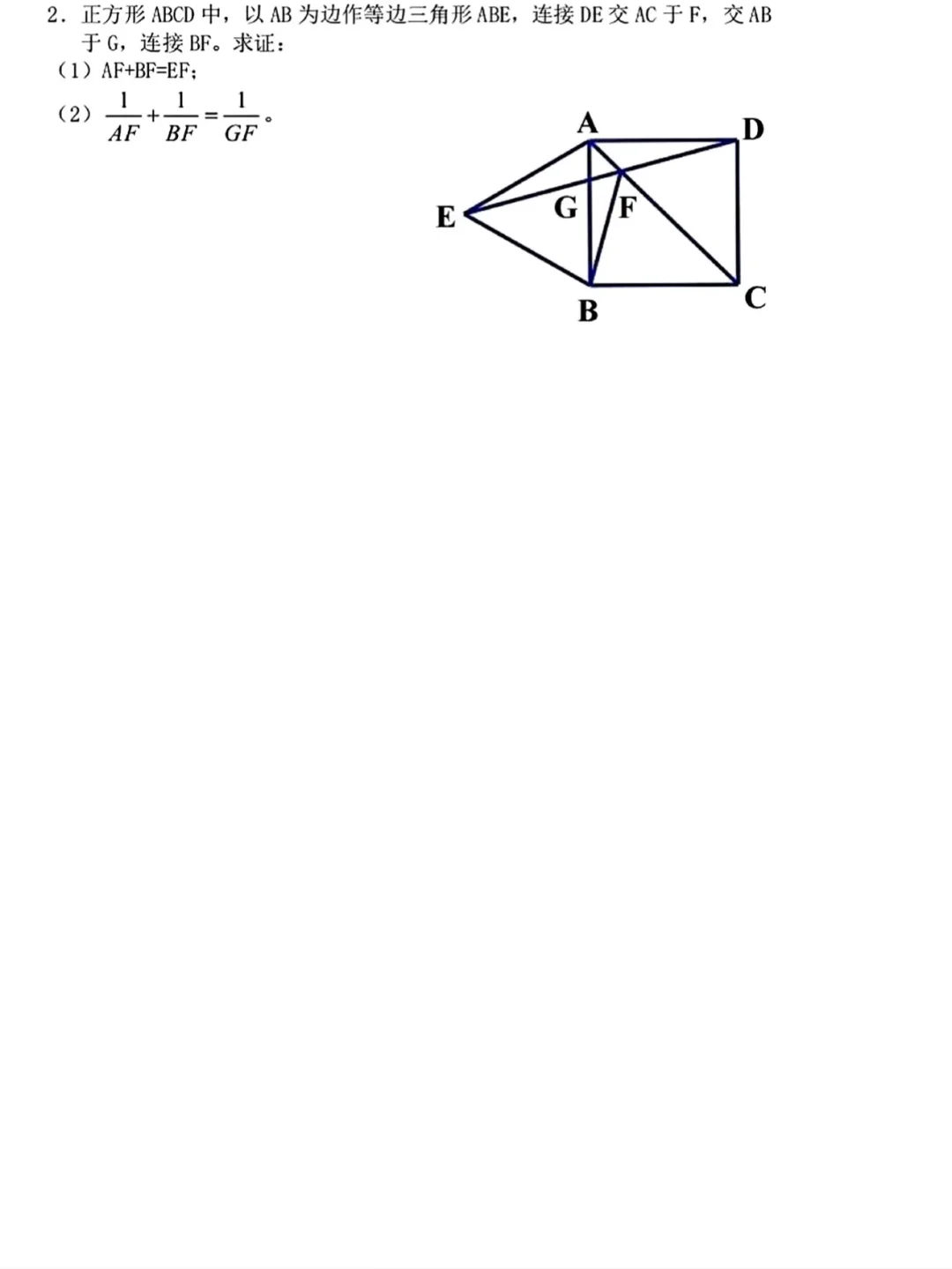
◦ A字型:一条直线平行于三角形的一边,与另外两边(或延长线)相交,形成的小三角形与原三角形相似(如DE∥BC,则△ADE∽△ABC)。
◦ 反A字型:两个三角形有一个公共角,且另有一组角相等(如∠A为公共角,∠ADE=∠B,则△ADE∽△ABC)。
• 8字型(含反8字型):
◦ 8字型:两条直线相交,连接对应端点形成两个三角形,若有一组对顶角和一组同位角/内错角相等(如AB∥CD,∠AOB=∠COD,则△AOB∽△COD)。
◦ 反8字型:两条直线相交,形成的两个三角形有一组对顶角,且另有一组角相等(如∠AOB=∠COD,∠A=∠C,则△AOB∽△COD)。
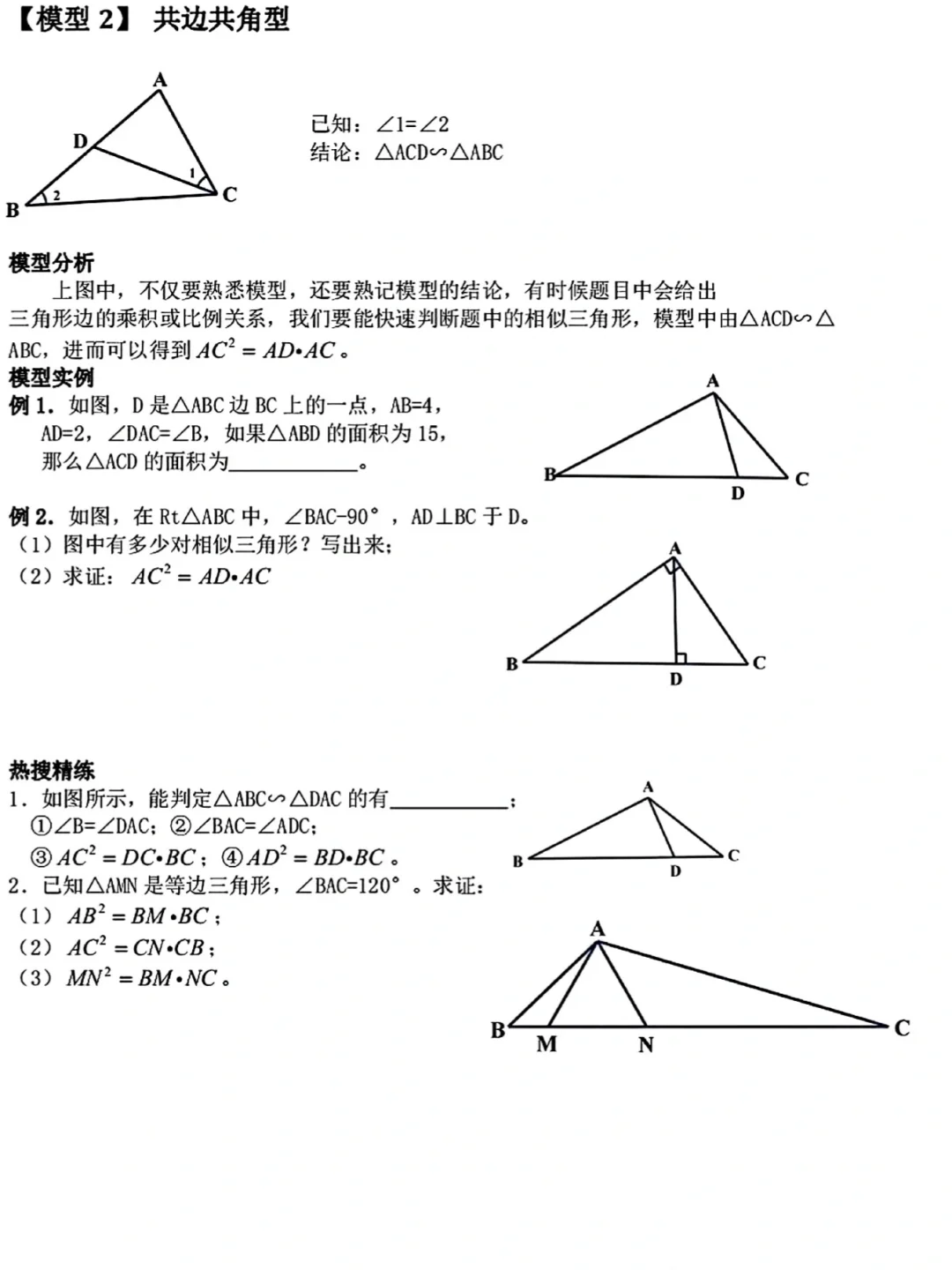
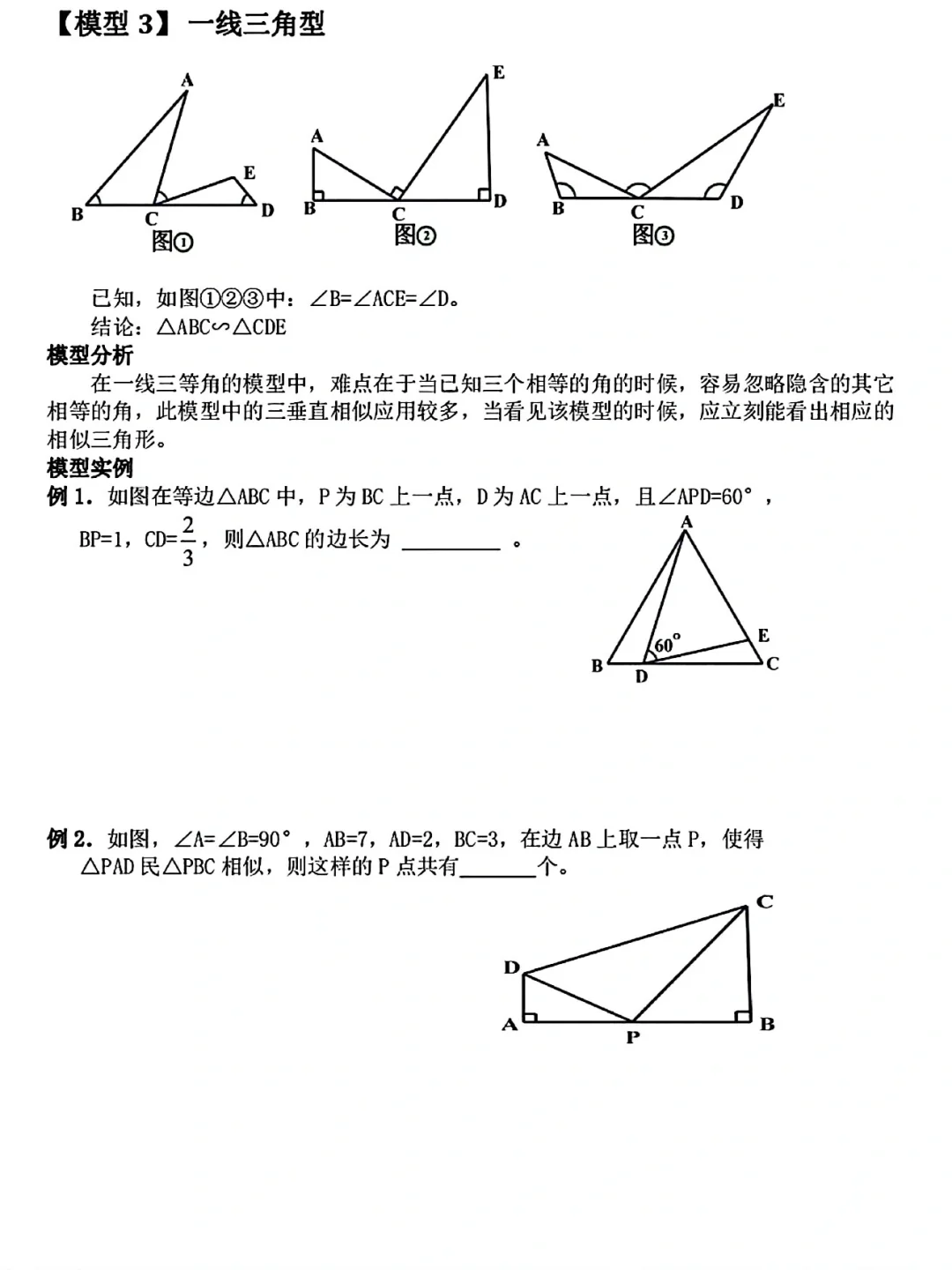
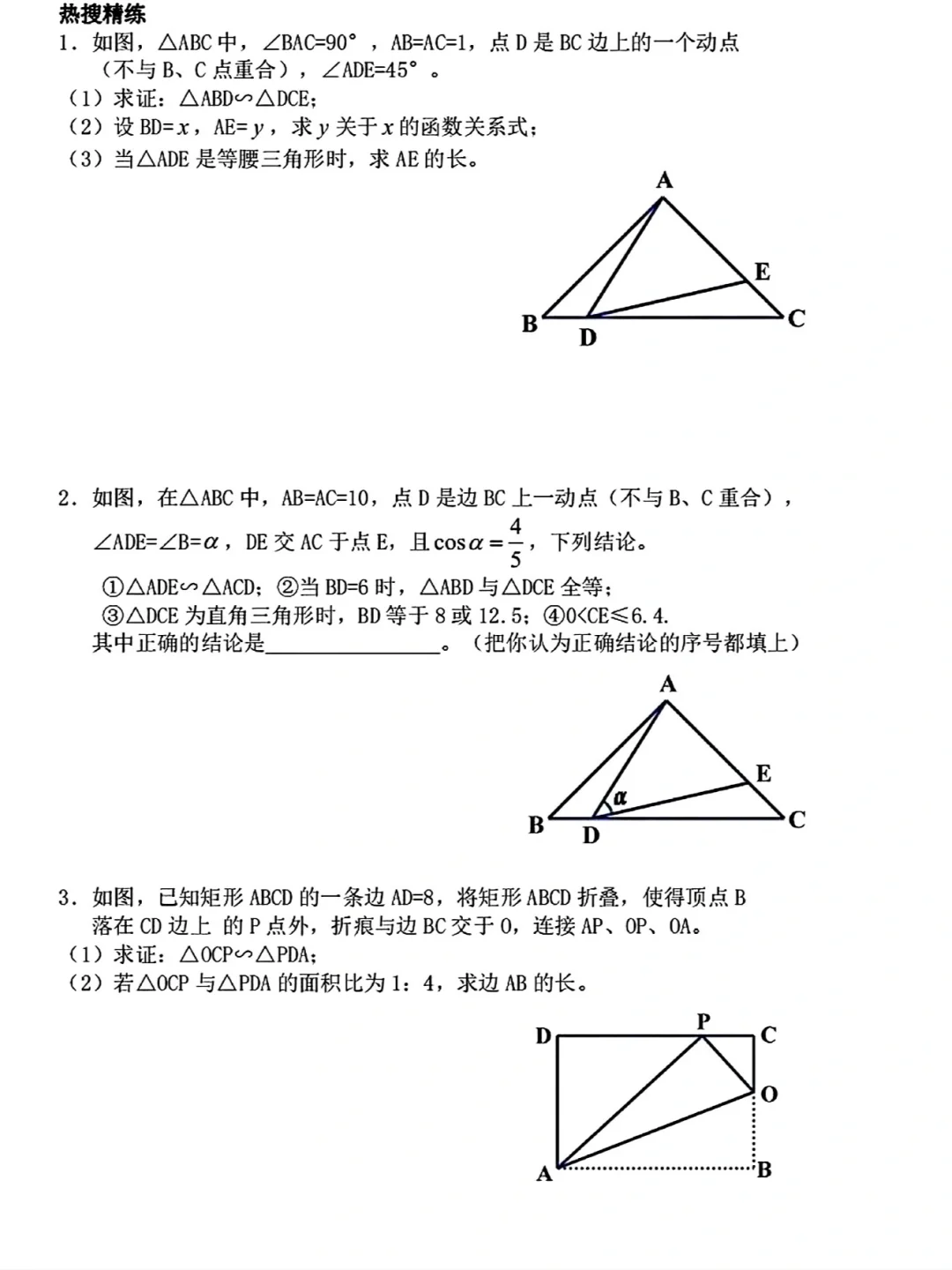
• 一线三等角模型:一条直线上有三个相等的角(如∠B=∠C=∠ADE),则两侧的三角形相似(△ABD∽△DCE),常见于等腰三角形、矩形、正方形中。
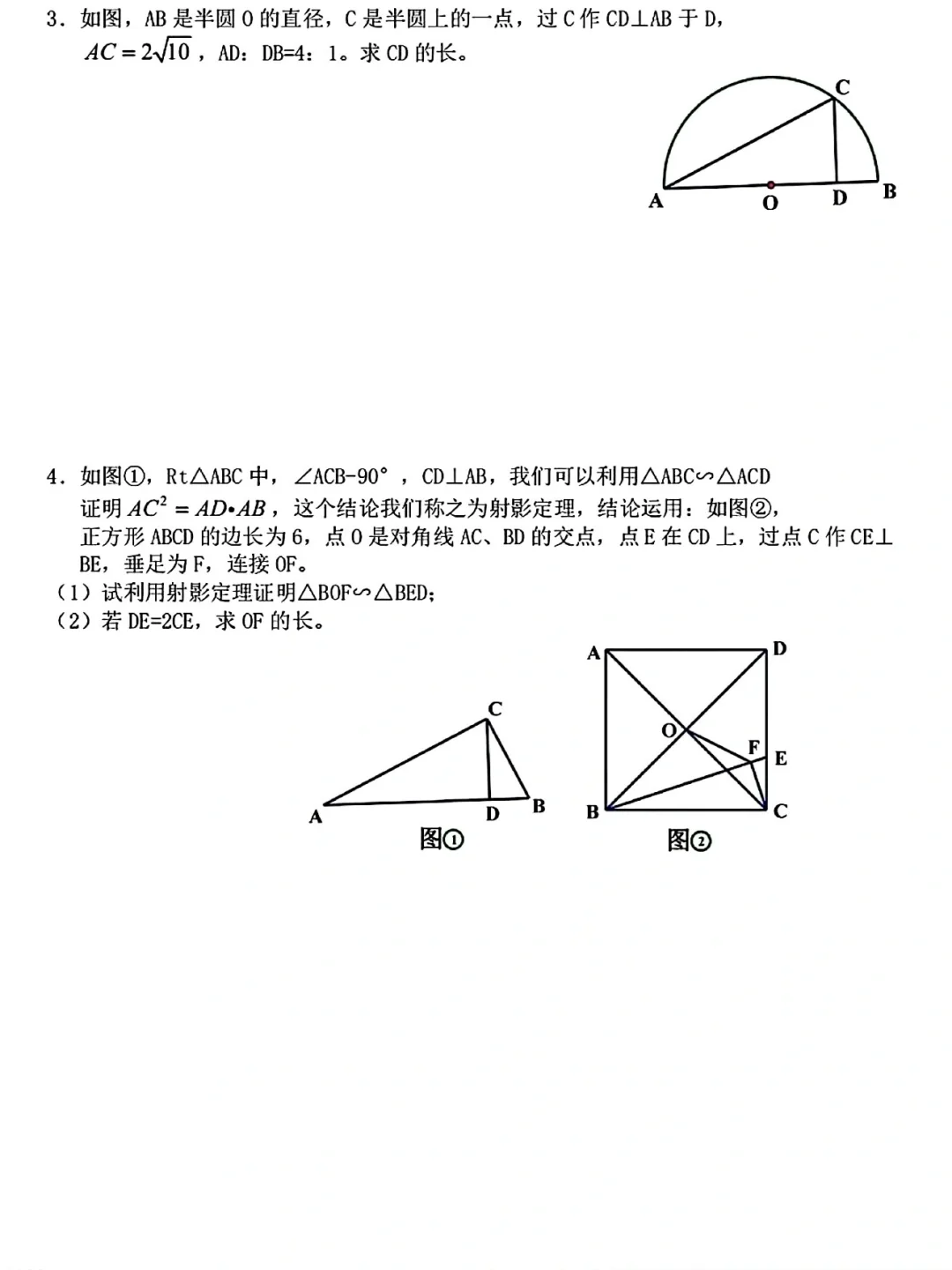
• 母子型相似(射影定理模型):直角三角形斜边上的高,将原三角形分成两个小直角三角形,这三个直角三角形两两相似(如Rt△ABC中,CD⊥AB,则△ABC∽△ACD∽△CBD),由此可推导出射影定理。#数学 #初中数学知识点 #中考数学几何模型 #半角模型#相似模型
最典型的是“90°含45°”模型(如正方形中)和“120°含60°”模型(如等边三角形中),解题思路高度统一:
1. 旋转构造:将半角旁边的一个三角形绕顶点旋转,使与半角相关的两条相等线段重合。
2. 证明全等:旋转后,新形成的三角形与半角另一侧的三角形全等(通常用SAS判定)。
3. 推导结论:利用全等得到线段相等或角相等,进而推导出最终结论(如线段和差、角度关系等)。
初中阶段最核心的四大相似模型如下:
• A字型(含反A字型):
◦ A字型:一条直线平行于三角形的一边,与另外两边(或延长线)相交,形成的小三角形与原三角形相似(如DE∥BC,则△ADE∽△ABC)。
◦ 反A字型:两个三角形有一个公共角,且另有一组角相等(如∠A为公共角,∠ADE=∠B,则△ADE∽△ABC)。
• 8字型(含反8字型):
◦ 8字型:两条直线相交,连接对应端点形成两个三角形,若有一组对顶角和一组同位角/内错角相等(如AB∥CD,∠AOB=∠COD,则△AOB∽△COD)。
◦ 反8字型:两条直线相交,形成的两个三角形有一组对顶角,且另有一组角相等(如∠AOB=∠COD,∠A=∠C,则△AOB∽△COD)。
• 一线三等角模型:一条直线上有三个相等的角(如∠B=∠C=∠ADE),则两侧的三角形相似(△ABD∽△DCE),常见于等腰三角形、矩形、正方形中。
• 母子型相似(射影定理模型):直角三角形斜边上的高,将原三角形分成两个小直角三角形,这三个直角三角形两两相似(如Rt△ABC中,CD⊥AB,则△ABC∽△ACD∽△CBD),由此可推导出射影定理。#数学 #初中数学知识点 #中考数学几何模型 #半角模型#相似模型


