















研究单位: 香港中文大学深圳分校数据科学学院
研究背景与问题描述: 在分布式网络中,多个代理通过协作来最小化一个目标函数。现有方法如DSMT虽能加速收敛,但在处理频繁高维模型传输时成本高昂。
解决方案: 提出局部动量跟踪算法(LMT),结合了局部更新与动量追踪策略及无循环Chebyshev加速技术。LMT允许每个代理在连续通信轮次之间执行多次本地更新,从而减少通信开销。
#学术分享 #论文解读 #人工智能
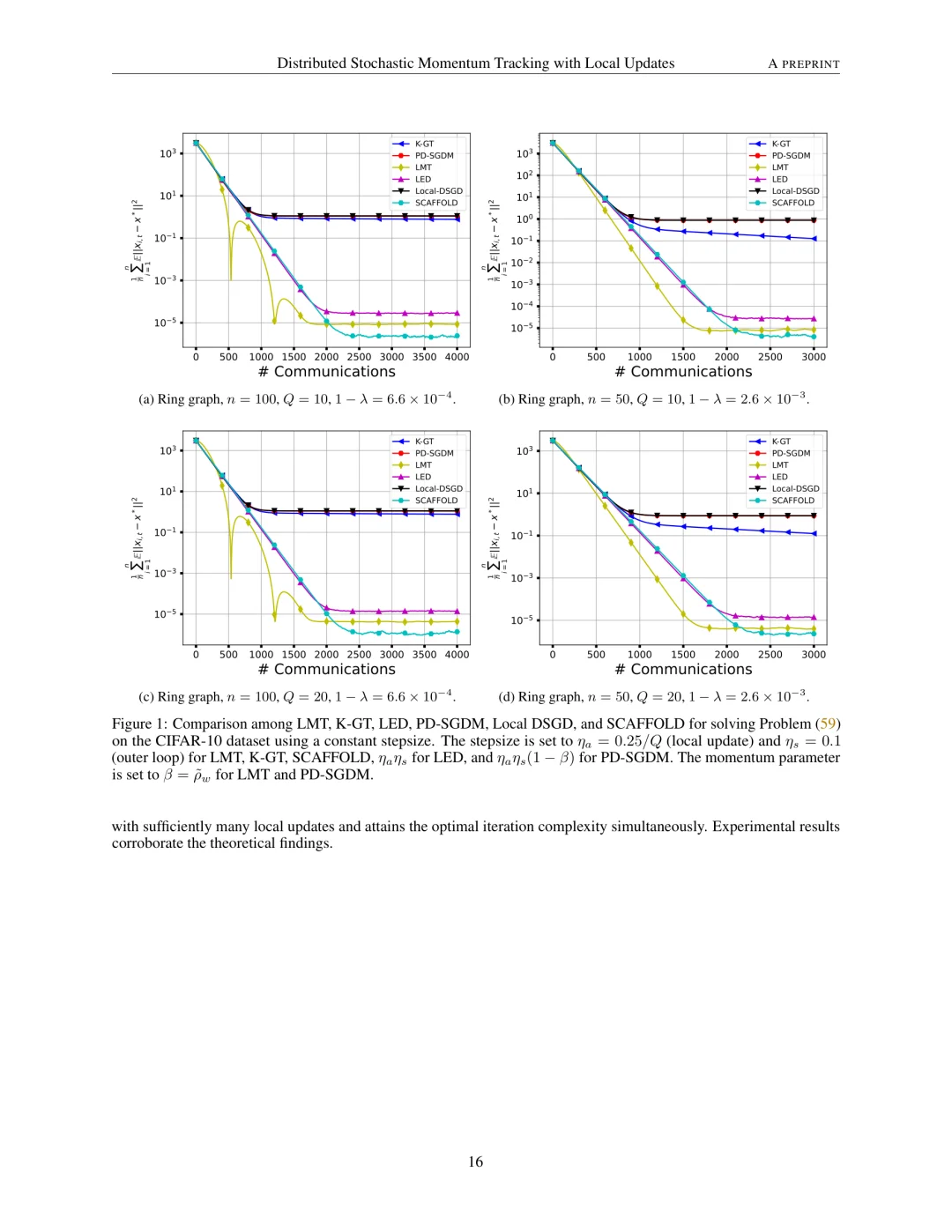
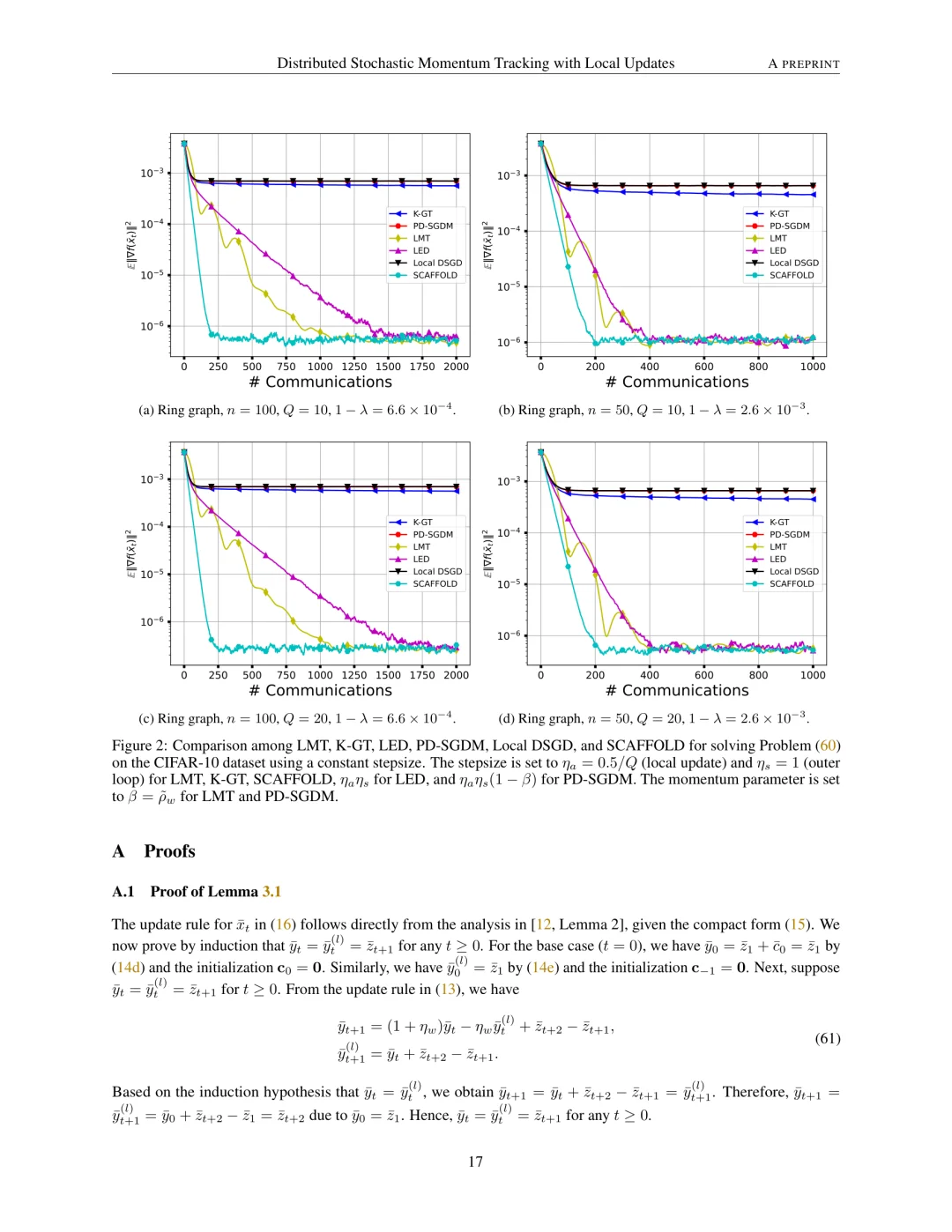
实验: 通过理论分析,证明了LMT在最小化平滑目标函数时能够实现线性加速。当本地更新次数足够多时,LMT达到了最优的通信复杂度;对于中等数量的本地更新,它实现了最优的迭代复杂度。
意义与影响: LMT是首个同时满足最优通信和迭代复杂度的方法,尤其适用于大规模分布式优化问题。
研究背景与问题描述: 在分布式网络中,多个代理通过协作来最小化一个目标函数。现有方法如DSMT虽能加速收敛,但在处理频繁高维模型传输时成本高昂。
解决方案: 提出局部动量跟踪算法(LMT),结合了局部更新与动量追踪策略及无循环Chebyshev加速技术。LMT允许每个代理在连续通信轮次之间执行多次本地更新,从而减少通信开销。
#学术分享 #论文解读 #人工智能
实验: 通过理论分析,证明了LMT在最小化平滑目标函数时能够实现线性加速。当本地更新次数足够多时,LMT达到了最优的通信复杂度;对于中等数量的本地更新,它实现了最优的迭代复杂度。
意义与影响: LMT是首个同时满足最优通信和迭代复杂度的方法,尤其适用于大规模分布式优化问题。


