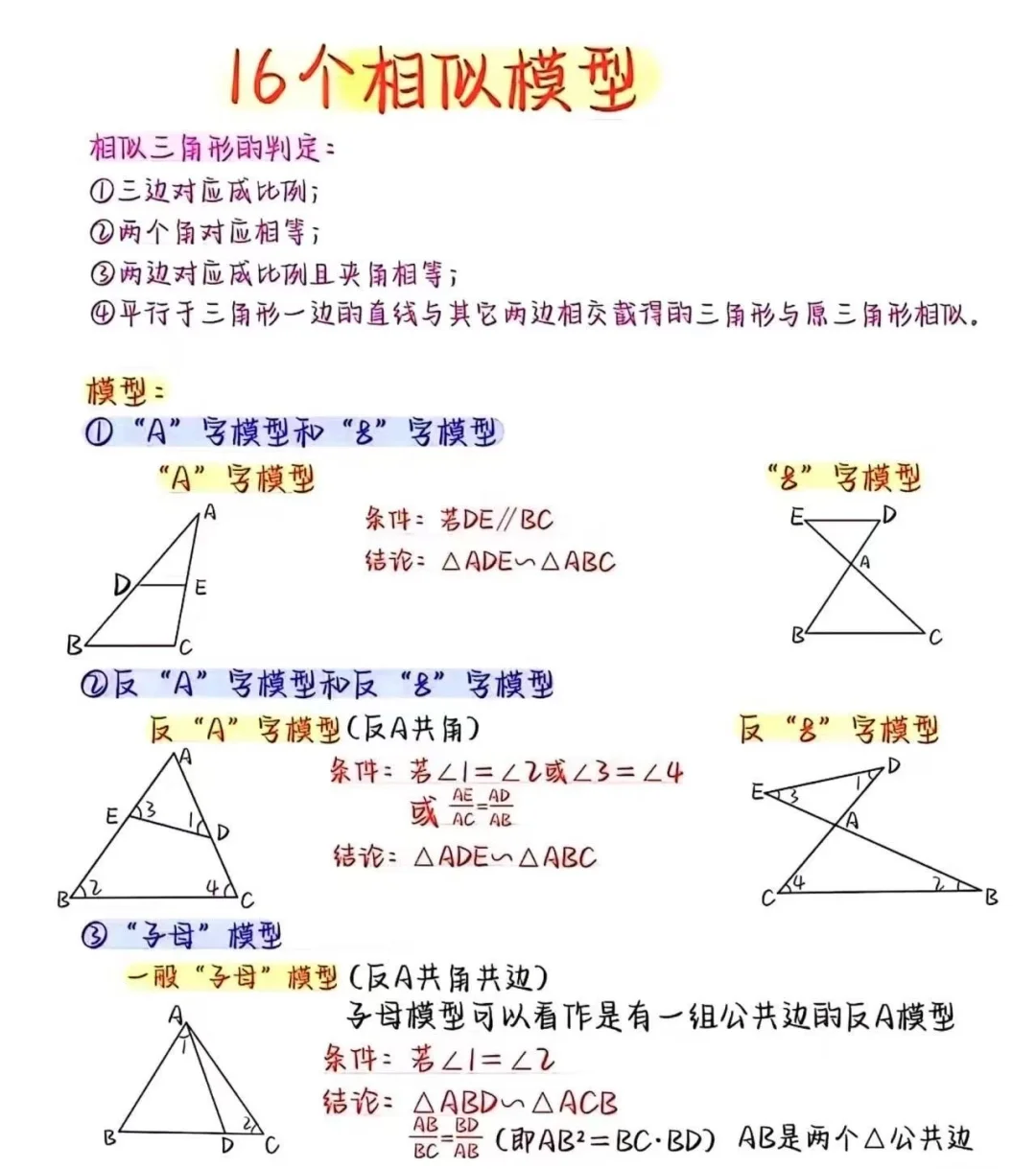
д»ҘдёӢжҳҜдёӯиҖғеёёиҖғзҡ„зӣёдјјдёүи§’еҪўдә”еӨ§еҹәжң¬жЁЎеһӢеҸҠе…¶зү№зӮ№пјҡ
?дёҖгҖҒAеӯ—еһӢжЁЎеһӢпјҲжӯЈAдёҺж–ңAпјү
зү№еҫҒпјҡ
?1. жңүдёҖдёӘе…¬е…ұи§’
?2. еҸҰдёҖз»„и§’еҜ№еә”зӣёзӯү
?3. йҖҡеёёжңүдёҖз»„иҫ№е№іиЎҢпјҲе№іиЎҢеҲҷеҝ…зӣёдјјпјү
еҸҳејҸпјҡжӯЈAеһӢпјҡDEвҲҘBC вҮ’ в–іADEвҲҪв–іABC
ж–ңAеһӢпјҡвҲ ADE=вҲ B вҮ’ в–іADEвҲҪв–іABCпјҲйңҖиҜҒжҳҺдёҖз»„и§’зӣёзӯүпјү
?дәҢгҖҒ8еӯ—еһӢжЁЎеһӢпјҲжӯЈ8дёҺж–ң8пјү
зү№еҫҒпјҡ
?1. дёӨз»„еҜ№и§’еҲҶеҲ«зӣёзӯүпјҲеҜ№йЎ¶и§’+еҸҰдёҖз»„и§’пјү
?2. йҖҡеёёжңүе№іиЎҢзәҝж—¶зӣёдјјжҜ”жӣҙжҳҺжҳҫ
еҸҳејҸпјҡжӯЈ8еһӢ**пјҡABвҲҘCD вҮ’ в–іAOBвҲҪв–іCOD
ж–ң8еһӢпјҡвҲ A=вҲ D вҮ’ в–іAOBвҲҪв–іDOC
?дёүгҖҒжҜҚеӯҗеһӢжЁЎеһӢпјҲе°„еҪұе®ҡзҗҶеҹәзЎҖпјү
зү№еҫҒпјҡ
?1. зӣҙи§’дёүи§’еҪўдёӯпјҢж–ңиҫ№дёҠзҡ„й«ҳеҲҶеҮәзҡ„дёӨдёӘе°Ҹдёүи§’еҪўдёҺеҺҹдёүи§’еҪўеқҮзӣёдјј
?2. е…ұдёүеҜ№зӣёдјјпјҡв–іACDвҲҪв–іABCвҲҪв–іCBD
з»“и®әпјҲе°„еҪұе®ҡзҗҶпјүпјҡ
- ACВІ = ADВ·AB
- BCВІ = BDВ·BA
- CDВІ = ADВ·DB
?еӣӣгҖҒж—ӢиҪ¬зӣёдјјжЁЎеһӢ
зү№еҫҒ
?1. дёӨдёӘзӣёдјјдёүи§’еҪўз»•е…¬е…ұйЎ¶зӮ№ж—ӢиҪ¬дёҖе®ҡи§’еәҰ
?2. еҜ№еә”иҫ№еӨ№и§’зӣёзӯү
?3. йңҖйҖҡиҝҮж—ӢиҪ¬иҜҒжҳҺе…ЁзӯүжҲ–зӣёдјј
?дә”гҖҒдёҖзәҝдёүзӯүи§’жЁЎеһӢ
зү№еҫҒпјҡ
?1. дёҖжқЎзӣҙзәҝдёҠжңүдёүдёӘзӯүи§’пјҲйҖҡеёёдёәзӣҙи§’жҲ–й”җи§’пјү
?2. дёӨдёӘдёүи§’еҪўеӣ зӯүи§’е…ізі»зӣёдјј и§ЈйўҳжҠҖе·§пјҡ
?1. ж Үи®°зӯүи§’пјҡз”ЁзӣёеҗҢз¬ҰеҸ·ж ҮеҮәеҜ№еә”зӣёзӯүзҡ„и§’
?2. жҜ”дҫӢеҢ№й…ҚпјҡзӣёдјјжҜ”=еҜ№еә”иҫ№д№ӢжҜ”=й«ҳд№ӢжҜ”=е‘Ёй•ҝд№ӢжҜ”
?3. йқўз§Ҝе…ізі»пјҡйқўз§ҜжҜ”=зӣёдјјжҜ”зҡ„е№іж–№
#еҲқдёӯж•°еӯҰ笔记 #дёүи§’еҪўзҡ„еӨ–и§’ #дёүи§’еҪўзҡ„зЁіе®ҡжҖ§ #дёӯиҖғж•°еӯҰ #еҮ дҪ• #еӣҫеҪўдёҺеҮ дҪ• #ж•°еӯҰжҖқз»ҙ
?дёҖгҖҒAеӯ—еһӢжЁЎеһӢпјҲжӯЈAдёҺж–ңAпјү
зү№еҫҒпјҡ
?1. жңүдёҖдёӘе…¬е…ұи§’
?2. еҸҰдёҖз»„и§’еҜ№еә”зӣёзӯү
?3. йҖҡеёёжңүдёҖз»„иҫ№е№іиЎҢпјҲе№іиЎҢеҲҷеҝ…зӣёдјјпјү
еҸҳејҸпјҡжӯЈAеһӢпјҡDEвҲҘBC вҮ’ в–іADEвҲҪв–іABC
ж–ңAеһӢпјҡвҲ ADE=вҲ B вҮ’ в–іADEвҲҪв–іABCпјҲйңҖиҜҒжҳҺдёҖз»„и§’зӣёзӯүпјү
?дәҢгҖҒ8еӯ—еһӢжЁЎеһӢпјҲжӯЈ8дёҺж–ң8пјү
зү№еҫҒпјҡ
?1. дёӨз»„еҜ№и§’еҲҶеҲ«зӣёзӯүпјҲеҜ№йЎ¶и§’+еҸҰдёҖз»„и§’пјү
?2. йҖҡеёёжңүе№іиЎҢзәҝж—¶зӣёдјјжҜ”жӣҙжҳҺжҳҫ
еҸҳејҸпјҡжӯЈ8еһӢ**пјҡABвҲҘCD вҮ’ в–іAOBвҲҪв–іCOD
ж–ң8еһӢпјҡвҲ A=вҲ D вҮ’ в–іAOBвҲҪв–іDOC
?дёүгҖҒжҜҚеӯҗеһӢжЁЎеһӢпјҲе°„еҪұе®ҡзҗҶеҹәзЎҖпјү
зү№еҫҒпјҡ
?1. зӣҙи§’дёүи§’еҪўдёӯпјҢж–ңиҫ№дёҠзҡ„й«ҳеҲҶеҮәзҡ„дёӨдёӘе°Ҹдёүи§’еҪўдёҺеҺҹдёүи§’еҪўеқҮзӣёдјј
?2. е…ұдёүеҜ№зӣёдјјпјҡв–іACDвҲҪв–іABCвҲҪв–іCBD
з»“и®әпјҲе°„еҪұе®ҡзҗҶпјүпјҡ
- ACВІ = ADВ·AB
- BCВІ = BDВ·BA
- CDВІ = ADВ·DB
?еӣӣгҖҒж—ӢиҪ¬зӣёдјјжЁЎеһӢ
зү№еҫҒ
?1. дёӨдёӘзӣёдјјдёүи§’еҪўз»•е…¬е…ұйЎ¶зӮ№ж—ӢиҪ¬дёҖе®ҡи§’еәҰ
?2. еҜ№еә”иҫ№еӨ№и§’зӣёзӯү
?3. йңҖйҖҡиҝҮж—ӢиҪ¬иҜҒжҳҺе…ЁзӯүжҲ–зӣёдјј
?дә”гҖҒдёҖзәҝдёүзӯүи§’жЁЎеһӢ
зү№еҫҒпјҡ
?1. дёҖжқЎзӣҙзәҝдёҠжңүдёүдёӘзӯүи§’пјҲйҖҡеёёдёәзӣҙи§’жҲ–й”җи§’пјү
?2. дёӨдёӘдёүи§’еҪўеӣ зӯүи§’е…ізі»зӣёдјј и§ЈйўҳжҠҖе·§пјҡ
?1. ж Үи®°зӯүи§’пјҡз”ЁзӣёеҗҢз¬ҰеҸ·ж ҮеҮәеҜ№еә”зӣёзӯүзҡ„и§’
?2. жҜ”дҫӢеҢ№й…ҚпјҡзӣёдјјжҜ”=еҜ№еә”иҫ№д№ӢжҜ”=й«ҳд№ӢжҜ”=е‘Ёй•ҝд№ӢжҜ”
?3. йқўз§Ҝе…ізі»пјҡйқўз§ҜжҜ”=зӣёдјјжҜ”зҡ„е№іж–№
#еҲқдёӯж•°еӯҰ笔记 #дёүи§’еҪўзҡ„еӨ–и§’ #дёүи§’еҪўзҡ„зЁіе®ҡжҖ§ #дёӯиҖғж•°еӯҰ #еҮ дҪ• #еӣҫеҪўдёҺеҮ дҪ• #ж•°еӯҰжҖқз»ҙ


