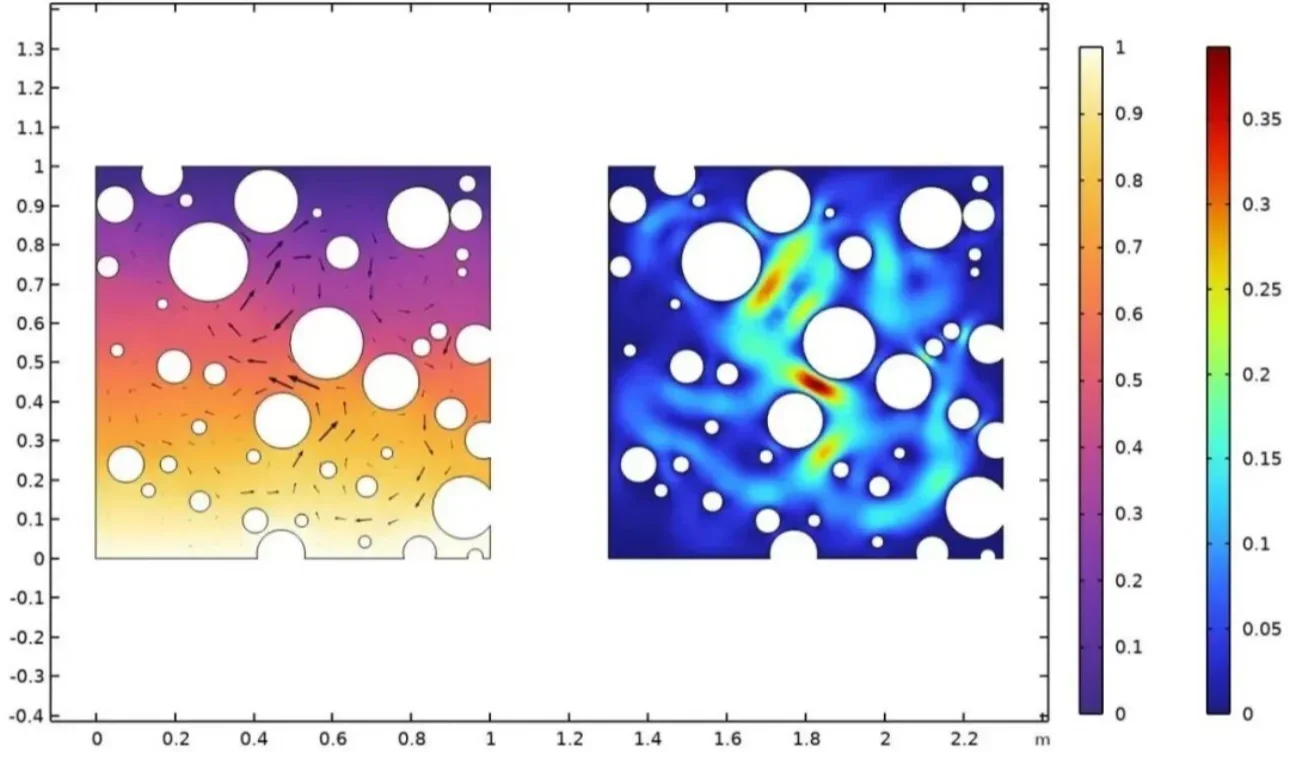
多孔介质是自然与工程中普遍存在的一类介质材料,其内部由复杂孔隙结构组成,流体在其中的运动与传热表现出独特规律。典型应用包括催化反应器、渗滤床、热交换器、地下水渗流以及多孔隔热材料等。由于孔隙尺度往往远小于工程尺度,直接对真实孔道几何进行数值模拟在计算上不可行,因此人们通常采用等效连续介质模型,将微观结构简化为具有等效阻力与传热特性的均质介质。在CFD软件(如Fluent)中,这一建模思想主要基于Darcy定律及其扩展形式
1.多孔介质流动模型的基本原理Darcy定律对于低速渗流,流体流速与压降成正比关系,其规律由Darcy定律描述:其中:Δp为单位长度压降;μ为流体动力黏度;v为体积平均速度;α为介质渗透率。该公式揭示了流动阻力与速度呈线性关系,适用于雷诺数较低、惯性效应可以忽略的情况。Forchheimer修正当流体速度升高时,孔隙内部局部加速和涡流不可忽视,此时需要在Darcy定律基础上加入惯性项,得到Darcy–Forchheimer方程:其中:C2为惯性阻力系数;ρ为流体密度第一项为黏性阻力第二项为惯性阻力,二者共同作用决定了流体在多孔介质中的压降规律。宏观平均方法上述方程来源于对微观Navier–Stokes方程进行体积平均处理。通过将流体变量在代表性体积单元内平均,可以得到修正的控制方程。结果表明,多孔介质宏观模型在数学上表现为动量方程中的附加源项,其形式与Darcy–Forchheimer方程一致。
2.参数计算方法渗透率(Permeability, α)渗透率反映多孔介质对流体通透性的能力,其值取决于孔径大小、连通性及几何形态。Kozeny–Carman方程(适用于均匀球形颗粒填充介质):其中ε为孔隙率,dp为颗粒直径。实验测定法:在低速条件下测量不同流量对应的压降利用Darcy定律线性拟合即可求得渗透率。经验数据库:对于常见工业材料,如金属泡沫、陶瓷滤材可直接查阅实验数据。惯性阻力系数(Inertial Resistance, C2)惯性阻力与孔隙几何结构、流动收缩扩张程度密切相关。Ergun方程(广泛用于颗粒堆积床):与Darcy–Forchheimer方程对比可得:实验法:通过拟合高流速区压降曲线的二次项,分离出惯性阻力系数孔隙率(Porosity,ε)孔隙率定义为:它决定了流体可利用的通道体积分数同时影响流动和传热。
1.多孔介质流动模型的基本原理Darcy定律对于低速渗流,流体流速与压降成正比关系,其规律由Darcy定律描述:其中:Δp为单位长度压降;μ为流体动力黏度;v为体积平均速度;α为介质渗透率。该公式揭示了流动阻力与速度呈线性关系,适用于雷诺数较低、惯性效应可以忽略的情况。Forchheimer修正当流体速度升高时,孔隙内部局部加速和涡流不可忽视,此时需要在Darcy定律基础上加入惯性项,得到Darcy–Forchheimer方程:其中:C2为惯性阻力系数;ρ为流体密度第一项为黏性阻力第二项为惯性阻力,二者共同作用决定了流体在多孔介质中的压降规律。宏观平均方法上述方程来源于对微观Navier–Stokes方程进行体积平均处理。通过将流体变量在代表性体积单元内平均,可以得到修正的控制方程。结果表明,多孔介质宏观模型在数学上表现为动量方程中的附加源项,其形式与Darcy–Forchheimer方程一致。
2.参数计算方法渗透率(Permeability, α)渗透率反映多孔介质对流体通透性的能力,其值取决于孔径大小、连通性及几何形态。Kozeny–Carman方程(适用于均匀球形颗粒填充介质):其中ε为孔隙率,dp为颗粒直径。实验测定法:在低速条件下测量不同流量对应的压降利用Darcy定律线性拟合即可求得渗透率。经验数据库:对于常见工业材料,如金属泡沫、陶瓷滤材可直接查阅实验数据。惯性阻力系数(Inertial Resistance, C2)惯性阻力与孔隙几何结构、流动收缩扩张程度密切相关。Ergun方程(广泛用于颗粒堆积床):与Darcy–Forchheimer方程对比可得:实验法:通过拟合高流速区压降曲线的二次项,分离出惯性阻力系数孔隙率(Porosity,ε)孔隙率定义为:它决定了流体可利用的通道体积分数同时影响流动和传热。